7 Нормальное распределение и стандартизация

7.1 Нормальное распределение и его свойства

Мы уже обсуждали нормальное распределение, когда говорили про распределения в целом [# Распределения]. Это вероятностный закон, где заданным значениям признака приводится в соответствие вероятность встретить признак с таким значением, выраженный по формуле \(P(x) = \frac{1}{\sigma\sqrt{2\pi}} * e^{-\frac{(x - \mu)^2}{2(\sigma)^2}}\)

Если внимательно посмотреть на формулу нормального распределения, можно обратить внимание, что почти все в ней является константами, кроме переменной \(x\) и двух неизвестных параметров: \(\mu\) и \(\sigma\). Это уже знакомые наши друзья: среднее генеральной совокупности (математическое ожидание и стандартное отклонение генеральной совокупности. Таким образом, чтобы построить распределение для любого признака, который в генеральной совокупности распределен нормально, нам необходимо знать только два параметра распределения:

среднее
стандартное отклонение

Помимо, собственно, формулы, часто можно увидеть такую запись, обозначающую нормальное распределение: \(\sim \mathcal{N}(\mu, \, \sigma^2)\)

На рисунке видно, что среднее отвечает за положение цента распределения, а стандартное отклонение – за его “растянутость” вдоль оси \(х\), ширину колокола.

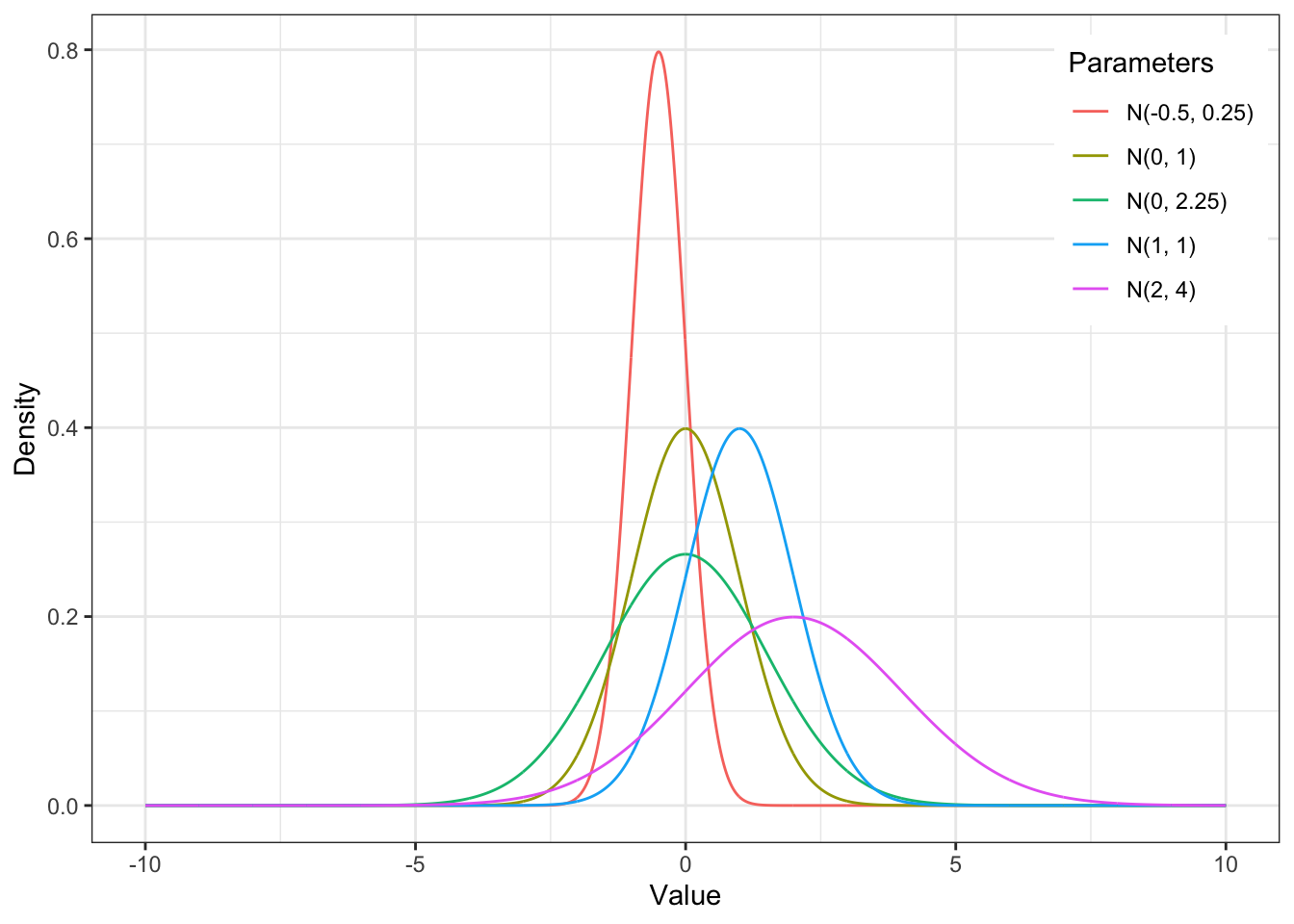Изображение из википедии

Почему такое внимание мы уделяем именно нормальному распределению?

Нормальное распределение интересно нам как минимум потому, что большинство признаковв, которые мы исследуем, являются случайными величинами, на которые действует большое количество случайныз факторов – а значит, согласно центальной предельной теореме, распределены номрально. Как следствие, физические, биологические и психологические признаки (рост, вес, выраженность черт личности) обычно распределены нормально: средние признаки встречаются в природе чаще, чем более радикальные
Нормальное распределение симметично и унимодально, и в некоторых операциях с ним попроще работать.
Для того, чтобы оценить вероятность встетить человека определенного роста, нам нужно знать (или оценить) только среднее и стандартное отклонение генеральной совокупности – и далее мы вычислим эту вероятность по формуле нормального распределения.

Нормальное распределение обладает рядом свойств:

симметрично
унимодально (только одна мода)
отклонения от среднего подчинаются вероятностному закону: знаем, сколько процентов данных содержится в скольких стандартных отклонения от среднего

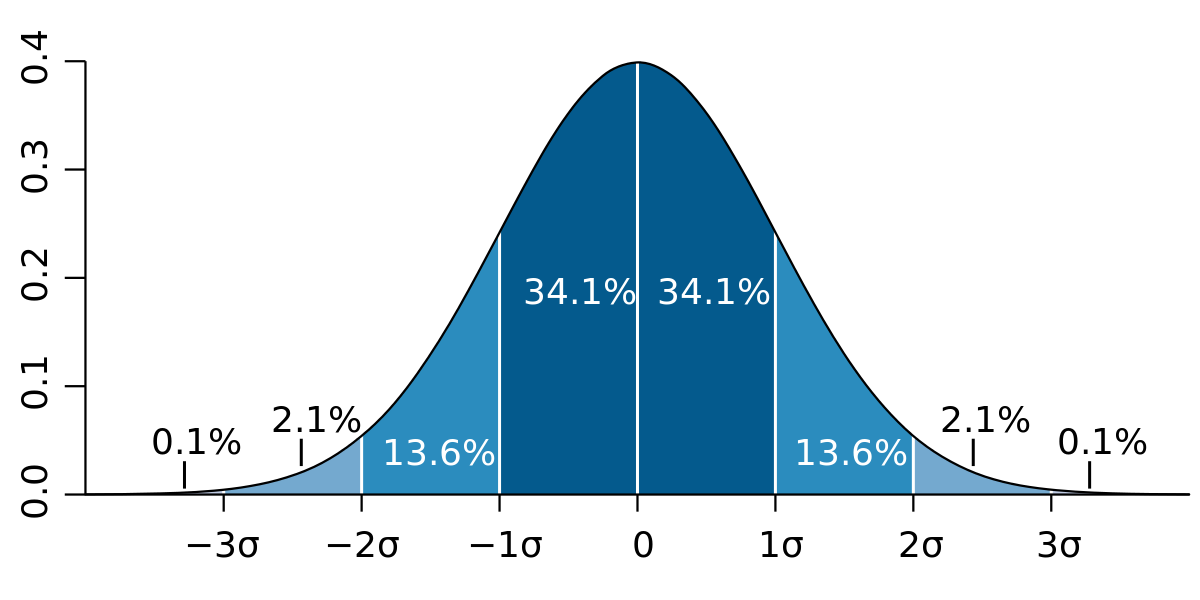
Последнее свойство дает нам очень большие возможности при работе с нормальным распределением: например, имея репрезентативную выборку замеров роста, мы можем посчитать, с какой вероятностью, например, встетим женщину с ростом 158 см. Вспоминаем визуализацию из первых семинаров https://ourworldindata.org/human-height

Чтобы посчитать эту вероятность, нам, по сути, нужно в формулу нормального распределения в качестве \(x\) вставить \(x=158\), а в качестве \(\mu\) и \(\sigma\) использовать выборочные средние и стандартные отклонения.

Некоторые значения процентов из этого распределения нужно запомнить, так как они будут встечаться часто – это значения для количества данных, лежащих внутри одного или нескольких стандартных отклонений от среднего.

“Правило трех сигм”:

в пределах одного стандартного отклонения от среднего значения (\(\bar x ± \sigma\)) лежит 68% значений — это очень частые значения;
в пределах двух стандартных отклонений от среднего значения (\(\bar x ± 2\sigma\)) лежит 95% значений — бо́льшая часть выборки;
в пределах трех стандартных отклонений от среднего значения (\(\bar x ± 3\sigma\)) лежит практически 100% выборки — то есть вся выборка.

7.2 Стандартное нормальное распределение (z-распределение)

Что делать, если нам нужно оценить, какая вероятность больше: встретить женщину ростом 158 см или мужчину ростом 174 см? Как видим из вузаилизации выше, эти распределения немного отличаются, и мы не можем расположить эти значения на одном. Здесь на помощь нам приходит стандартное нормальное распределение или z-распределение

Стандартное нормальное распределение – это нормальное распределение c центром в нуле (\(\mu=0\)) и стандартным отклонением равным 1 (\(\sigma=1\)).

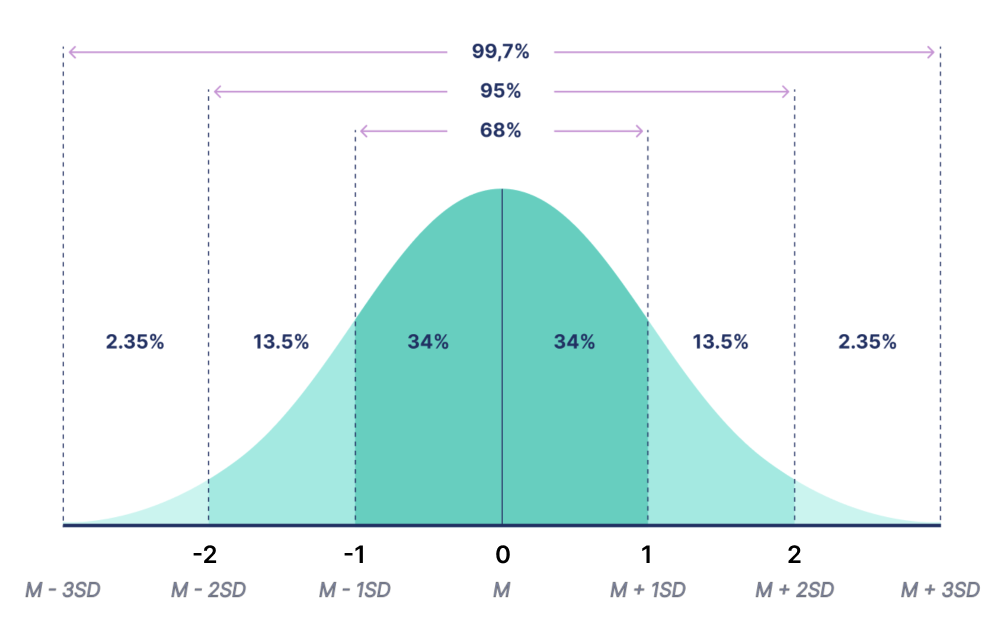
Это распределение универсально и безразмерно: на шкале у нас уже не \(\sigma\), а цифры, не имеющие размерности. Эта шкала назвается z-шкалой, а само распределение так же называется z-распределением. Любое нормальное распределение можно привести к виду стандартного нормального – это процедура называется z-преобразованием

7.3 Z-преобразование и стандартизация

Стандартизация – это процесс преобразования нормального распределения к стандартной безразмерной Z-шкале со средним 0 и стандартным отклонением 1.

Чтобы провести стандартизацию, нужно сделать две вещи:

центрировать распределение — если оно было смещено от нуля (например, \(\mu=15\)), то нам нужно вернуть его в центр \(\mu=0\)
нормировать распределение — избавиться от разницы в отклонениях \(\sigma\), привести наше распределени к распределению с \(\sigma=1\)

Учитывая две эти операции, формула z-преобразования выглядит следующим образом:

\(Z_x = \frac{x - \mu}{\sigma}\)

Z-оценку можно расположить на Z-распределении и посмотреть, какой процент данных лежит левее Z-оценки, то есть менее вероятен. Высчитать этот процент можно по формуле нормального распределения, подставив \(\mu=0\) и \(\sigma=1\), но проще воспользоваться таблицами Z-оценок (они легко гуглятся), например https://www.z-table.com/

Стандартизация не меняет характер распределения, менят только положения его центра и “расплющенность” вдоль оси ч– то есть буквально то, что мы знаем по свойствам среднего и дисперсии

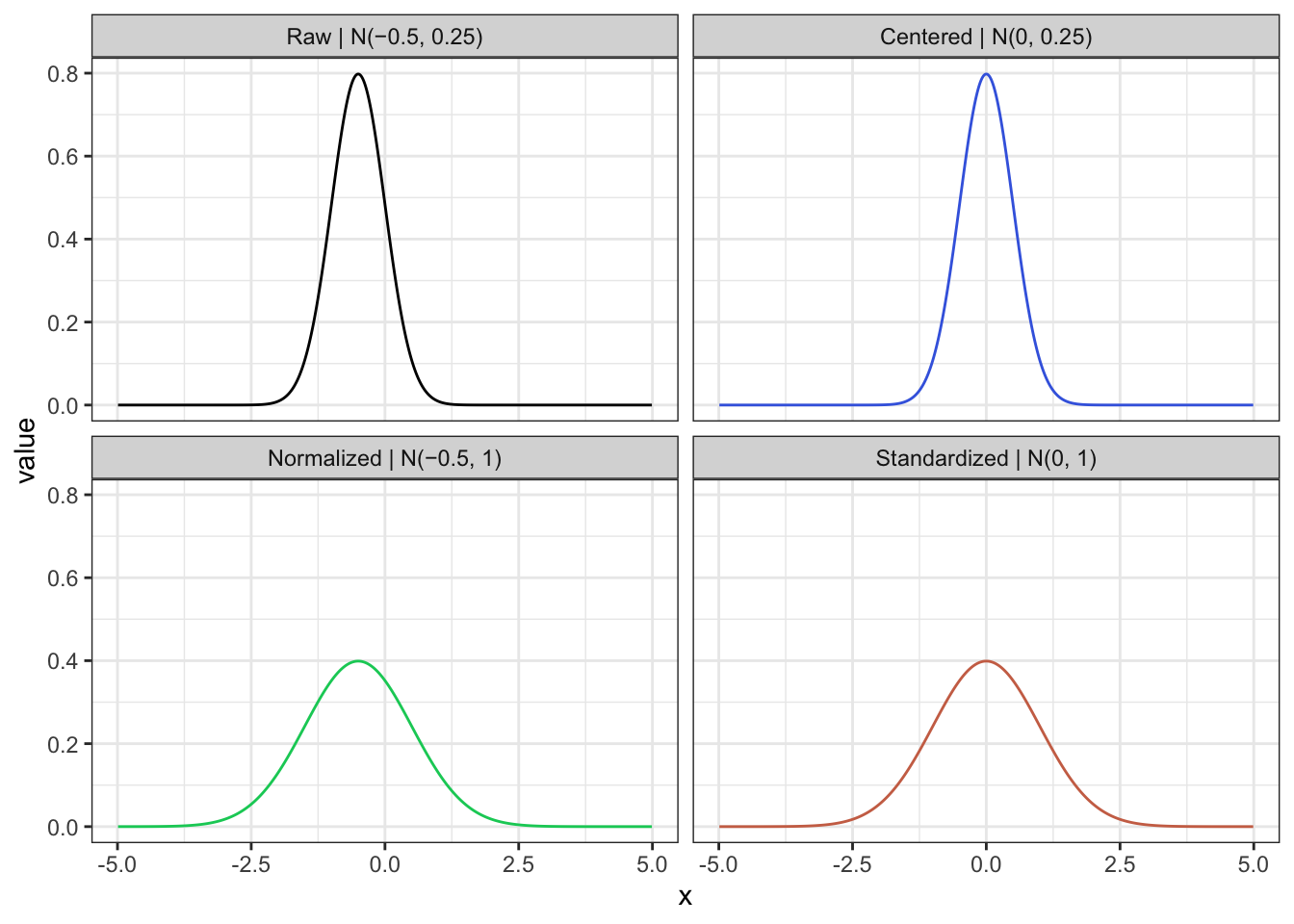
Можно интерпретировать Z-шкалу как шкалу типичности или частотности встечаемости значний: все, что лежит в +- 1 – встечается очень часто, и чем дальше от цента – тем более редкие значения нам попадаются.

Таким образм, Z-преобразование используется чтобы:

Узнать, насколько типично (частотно) встреченное нами значение
Сравнить вероятности встретить значения из двух разных выборок (нормально распределенных)

Например, мы (откуда-то) знаем, что средний рост женщин 165 см со стандартным отклонением 7, а средний рост мужчин – 178 и станд откл 8.

Возвращаясь к нашему вопросу:

\(Ж_{158}\): \(Z_{158} = \frac{x - \mu_ж}{\sigma_ж} = \frac{158 - 165}{7} = -1\)

\(М_{174}\): \(Z_{174} = \frac{x - \mu_м}{\sigma_м} = \frac{174- 178}{8} = -0.5\)

Мы перевели рост мужчин и женщи в Z-оценки и теперь можем расположить их на Z-распределнии. Уже видно, что число -1 располагается левее, чем число -0.5, значит, вероятность встретить женщину с ростом 158 см меньше, чем мужчину с ростом 174 см. Чтобы оценить эту вероятность точно, нам придется воспользоваться таблицами Z-оценок https://www.z-table.com/

\(Z_{ж_158} = -1\), что соответствует примерно 16% вероятности \(Z_{м_174} = -0.5\), что соответствует примерно 30% вероятности

Таким образом, вероятность встретить женщину с ростом 158 см составляет 16%, и это на 14% меньше, чем вероятность встретить мужчину ростом 174 см.