6 Описательная статистика

Мы переходим к обсуждению первого вида статистики из двух – описательной статистики (descriptive statistics). Когда мы гооворим об описательной статистике, мы всегда говорим об эмпричиески полученных данных, а не о генеральной совокупности. Чтобы что-то сказать о генеральной совокупности, нам нужно заниматься статистикой вывода, а пока остновимся на эмпирически полученных данных и выборочных распределениях.

Зачем нужна описательная статистика? Мы обсуждали, что описательная статистика:

  • описывает данные: мы исследуем сами переменные, смотрим на данные по ним и узнаем их получше
  • позволяет заменить набор данных на отдельные цифры – зачастую это проще для понимания и понятнее для восприятия, чем смотреть на табличку значений

Если вдруг так вышло, что наши собранные данные представляют собой всю генеральную совокупность, то нам даже не нужно заниматься статистикой вывоода – мы можем сделать какие-то выводы об этих данных уже из эмпирически собранных данных (например, сравнить успеваемость в классе A и Б всего одной школы)

6.1 Описательные визуализации

Мы уже обсуждали два важных графика – гистограмму и график плотности вероятности – когда говорили про распределения. Эти графики стоит строить каждый раз, когда мы хотим поисследовать эмпирически полученные данные методами описательной статистики. Такого термина, кажется, официально не существует, но я называю эти графики также описательными.

Например, мы строили их для данных про эмоциональное выгорание:

Для визуализации порядковой переменной Опыта преподавания exp_scaled

burnout %>% 
  ggplot(aes(x=exp_scaled)) +
  geom_bar() +
  theme_minimal()

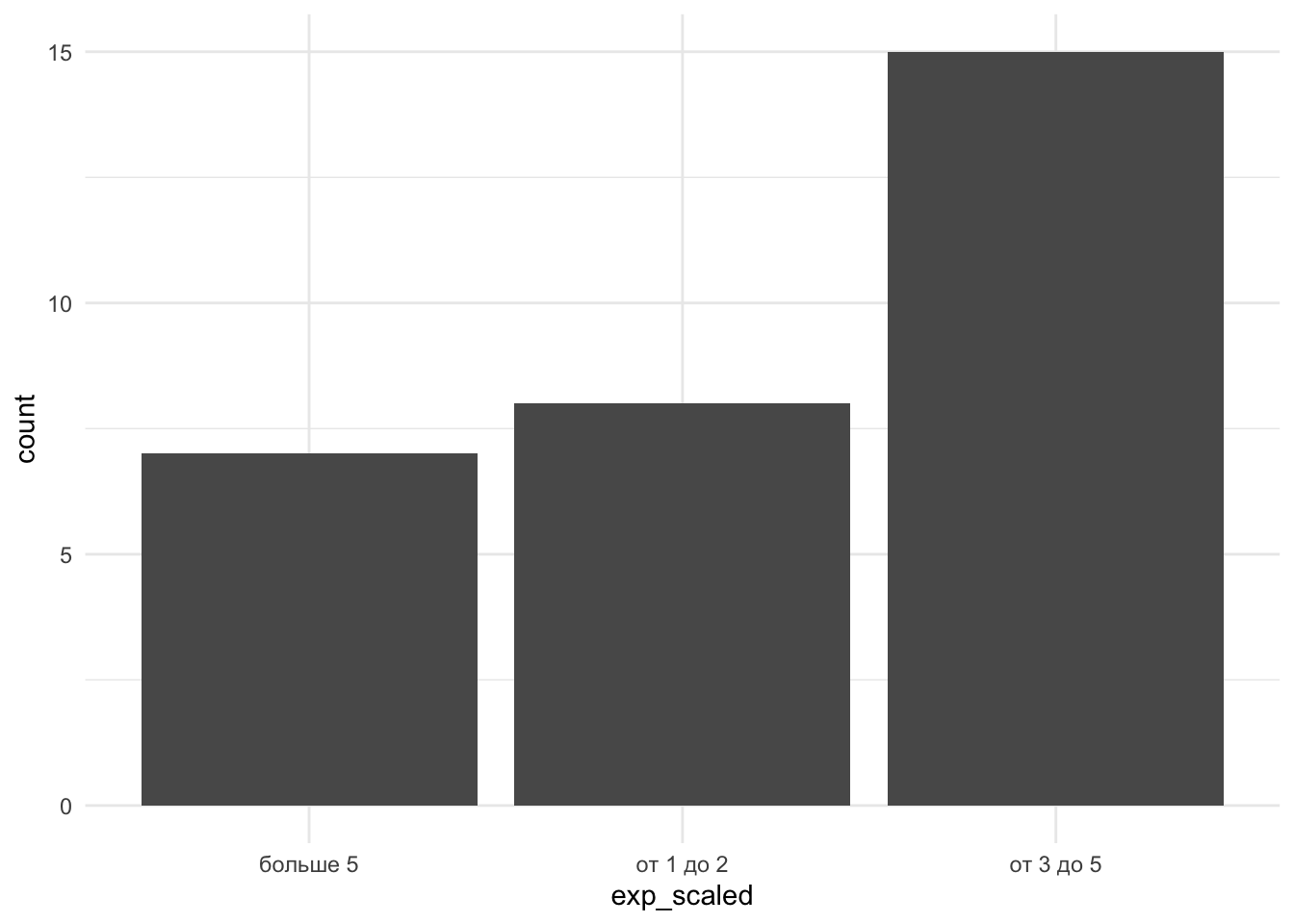
Для визуализации количественной переменной Возраст age (шкала отношений)

burnout %>% 
  ggplot(aes(x=age)) +
  geom_density() +
  theme_minimal()

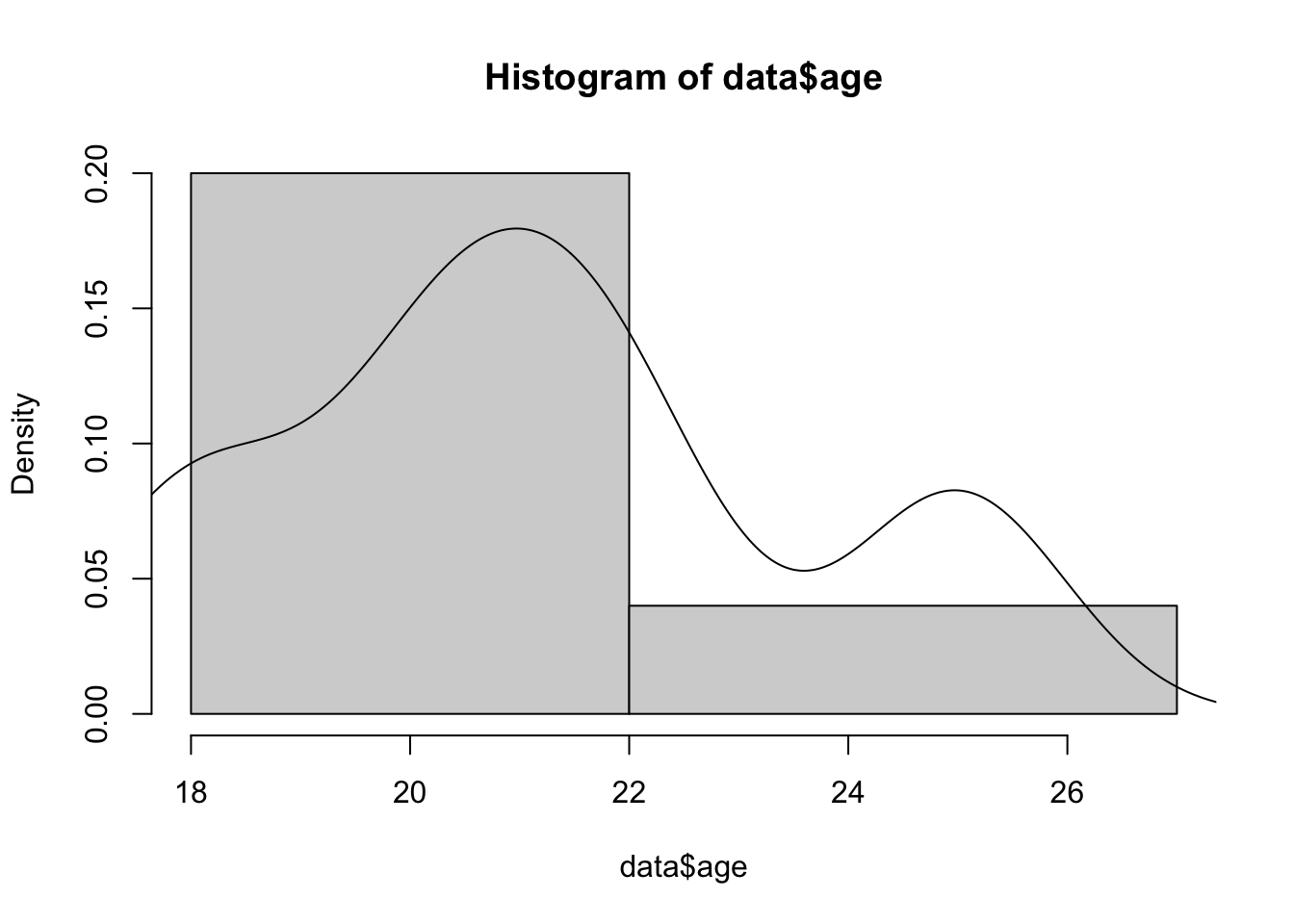
Графики распределений, на самом деле, уже дают нам многое – как миниум понимание, к какому семейству распределений может принадлежать переменная, и каковы свойства распредедения этих данных. Говоря о свойствах графиков, обычно имеются два.

Коэффициент ассиметрии, “скошенность” (skewness) – показатель симметричности графика: если график симметричен6 этот показатель равен 0, если нет, имеет значение отличное от нуля в ту сторону, в котороую график скошен.

  • Если коэффициент ассиметрии положительный, \(S > 0\) – говорят о правосторонней ассиметии (правая часть вытянута больше, чем левая).
  • Если коэффициент ассиметрии отрицательный, \(S < 0\) – говорят о левосторонней ассиметии (левая часть вытянута больше, чем правая).

Эксцесс, “вытянутость” (kurtosis) – показатель, насколько график вытянут вверх или “приплюснут” вдоль оси абсцисс.

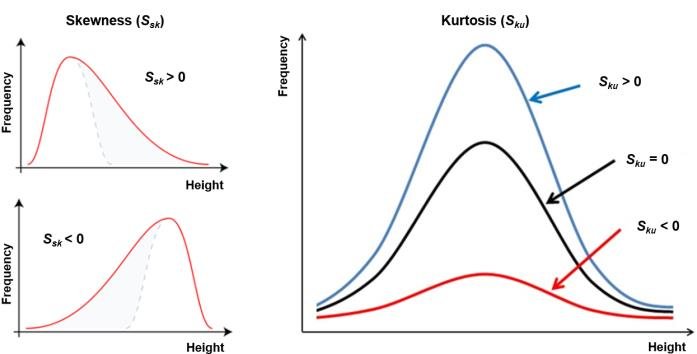
Если ## Меры центральной тенденции {#ctm}

Меры центральной тенденции – это такие описательные статистики, которые позволяют что-то сказать про “центр масс” распределения: где у него центр, где больше всего данных в этом распределении? Это бывает очень полезно на прикладных вопросах.

Представим, что нас интересует вопрос: каково благосостояние россиян? Изменилось ли оно с 2008 по 2022 год, и если да, то как? Как можно ответить на этот вопрос? (представим, что у нас есть доступ к реалистиным данными всех россиян, собранных по этому вопросу, и делать статистический вывод по небольшой выборке нет необходимости)

Допустим, будем оценивать благосостояние по годовому доходу на душу населения. Первое, что напрашивается – это посчитать среднее значение дохода в 2008 году и в 2022 году и посмотреть, как они отличаются. Правильный ли это будет расчет? Скорее всего, нет.

Дело в том, что доход на душу населения – очень неравномерный признак (переменная). https://ru.wikipedia.org/wiki/%D0%9A%D0%BE%D1%8D%D1%84%D1%84%D0%B8%D1%86%D0%B8%D0%B5%D0%BD%D1%82_%D0%94%D0%B6%D0%B8%D0%BD%D0%B8

6.1.1 Среднее, медиана, мода

Среднее арифметическое (mean) – сумма всех значений, поделенная на количество наблюдений. Вычисляется поо формуле \(\bar X = \dfrac{\sum_{i=1}^{n}x_i}{n}\)

Например, у нас есть набор данных:

##  [1] 49 37  1 25 10 36 18 24  7 45 47

Его среднее

mean(sample_data1)
## [1] 27.18182

Свойства среднего

Полезно помнить о свойствах среднего:

  1. Если к каждому значению выборки прибавить (или вычесть) одно и то же число, то среднее так же увеличится (или уменьшится) на это же число: \(\bar X_(x_i+c) = \bar X + c\)

  2. Если каждое значение выборки умножить (или разделить) одно и то же число, то среднее так же увеличится (или уменьшится) в это же число раз \(\bar X_(x_i \times c) = \bar X \times c\)

  3. Сумма всех отклонений от среднего равна нулю \(\sum_{i=1}^{n}(\bar X - x_i) = 0\)

Медиана (median) – это граница, которая делает упорядочненное множество данных пополам. Для того, чтобы посчитать медиану, нам нужно: 1) расставить все имеющиеся значения в порядке возрастания; 2) найти середину: это будет либо значение, соответствующее месту \(\frac{n}{2}+1\), если n – нечетное, либо среднее из двух центральных значений \((\frac{1}{2}(X_{n/2}+X_{n+1})/2\), если n – четное.

sort(sample_data1)
##  [1]  1  7 10 18 24 25 36 37 45 47 49
median(sample_data1)
## [1] 25
##  [1] 37 46 20 26  3 41 25 27 36 50
sort(sample_data2)
##  [1]  3 20 25 26 27 36 37 41 46 50
median(sample_data2)
## [1] 31.5

На практике нам редко встречаются данные, где каждое значение представлено только один раз – мы уже много обсуждали, что в статистике мы работаем с вероятностями и частотами. Поэтому в реальности нужно не забывать, что мы делим пополам не сами значения, как в случае с средним – а распределение значений. На гистограмме или графике плотности вероятности медиана – это линия, которая делит график на две равные по площади части: слева и справа должно остаться одинаковое число данных (значений, взятых с их частотами).

burnout %>% 
  ggplot(aes(x=exp_years)) +
  geom_histogram(binwidth = 1) +
  geom_vline(xintercept = median(exp_years)) +
  theme_minimal()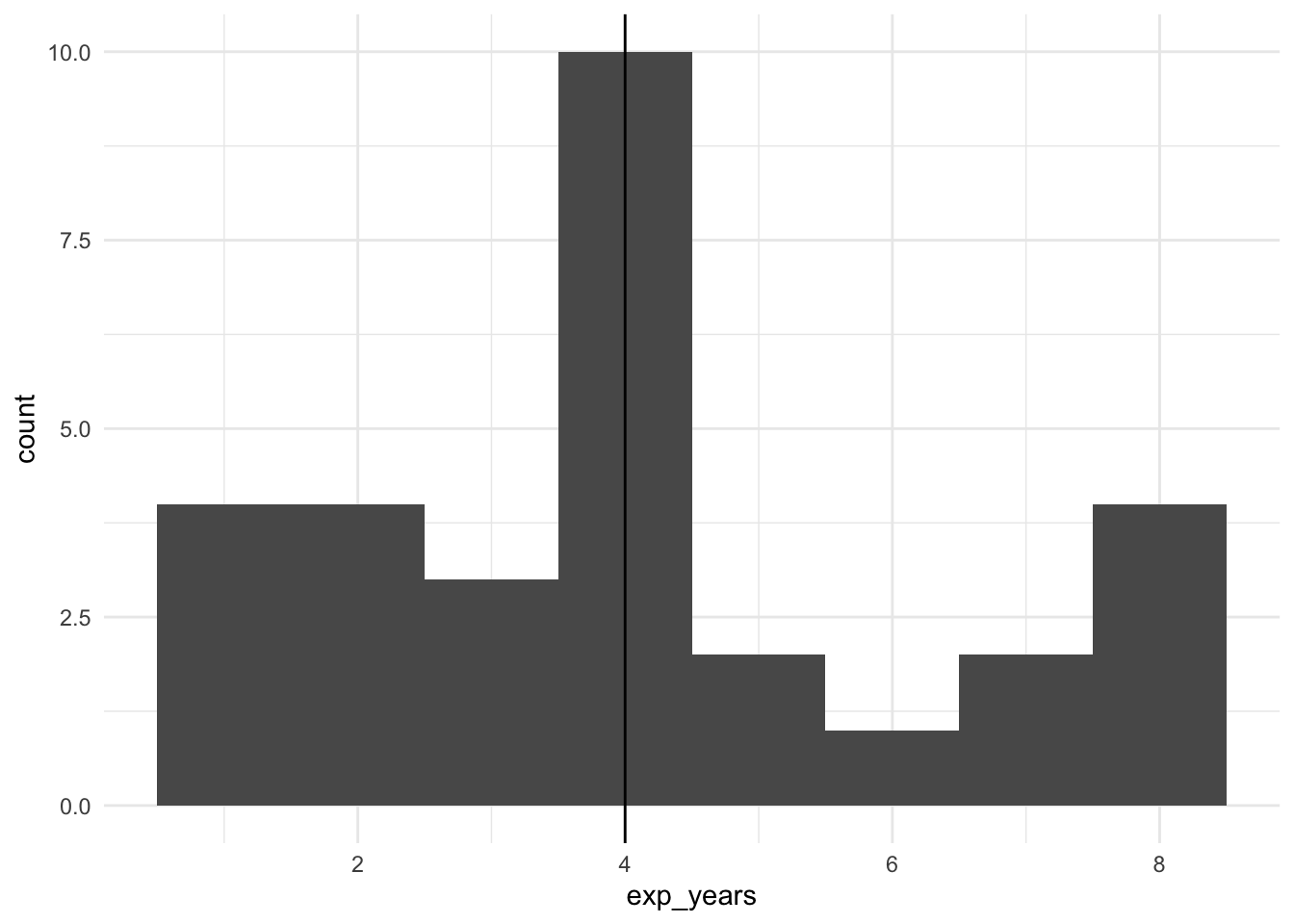

Мода (mode) – то значение признака, которое встречается чаще остальных.

На гистограмме мода вседа будет находиться на самом высоком стролбике, а на графике плотности вероятности – в его пике (или очень-очень близко к нему – помним, что график плотности вероятности – это финт ушами, где мы рисуем каждую точку как бы “забирая” с собой ее окрестность, поэтому в завиисомости от размера окрестности медиана может чуть-чуть поплыть от пика, но это крошечное отклонение)

Взвешенное среднее.

Квадратичное среднее.

6.1.2 Особенности использования

В примере с оценкой благосостояния мы выяснили, что среднее значение здесь – плохой выбор для описания этих данных с помощью мер центральной тенденции. Тогда какие меры центральной тенденции выбрать?

Мера ЦТ Данные и шкала Особенности использования
Среднее Только количественная: шкала отношений или интервальная достаточно большая выборка, распределение симметрично, нет заметных выборосов
Медиана Количественная или порядковая: шкала отношений, интервальная или порядковая (ранговая) можем использовать, когда распределение не симметрично, есть выбросы, не можем использовать для номинативной шкалы
Мода Любая шкала, Номинативная (номинальная), порядковая, количественная (отношений или интервальная) чаще всего используется там, где не можем производить метрические операции, но не можем точно посчитать моду для количественных непрерывных величин

Где на графиках среднее, медиана и мода?

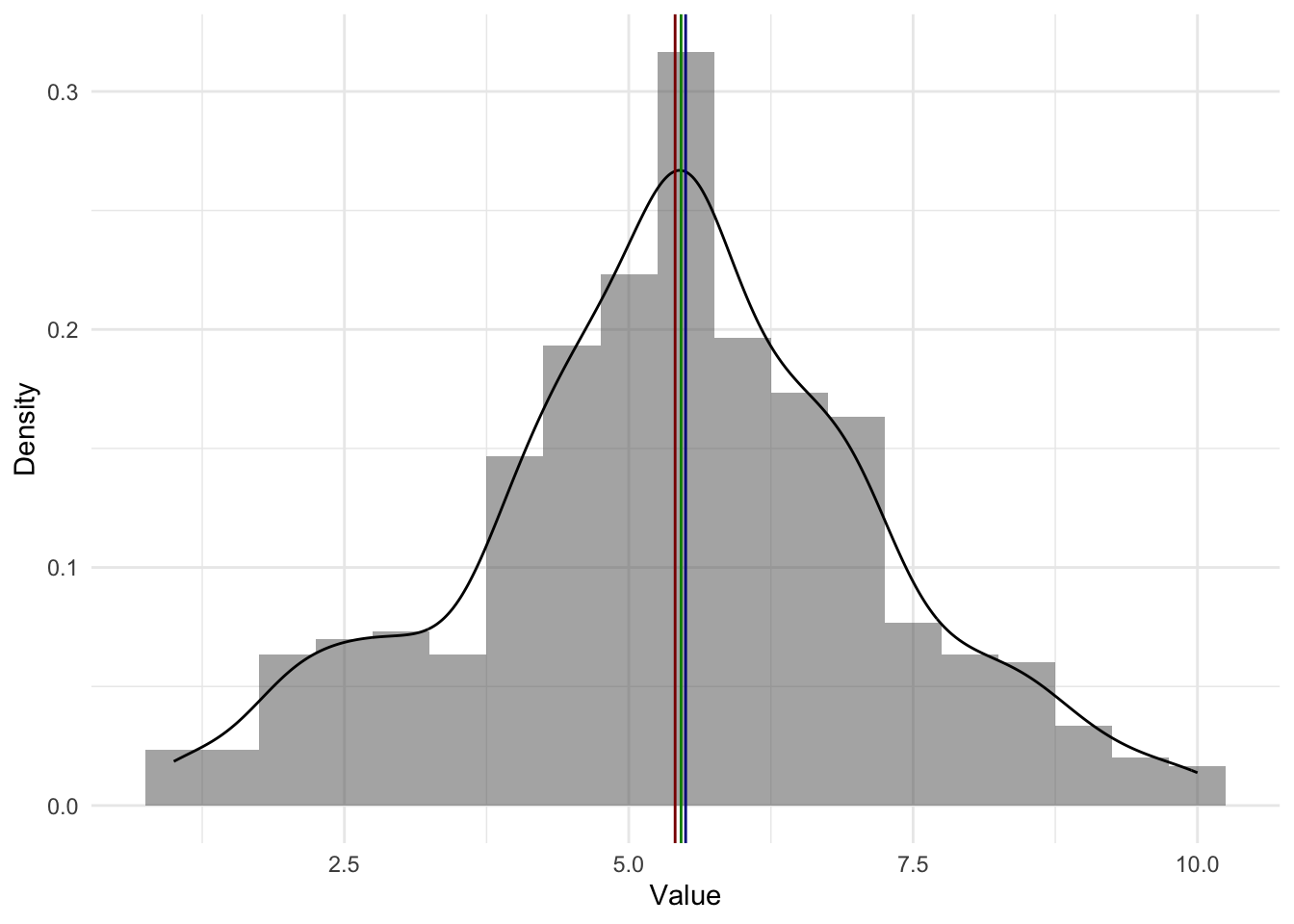
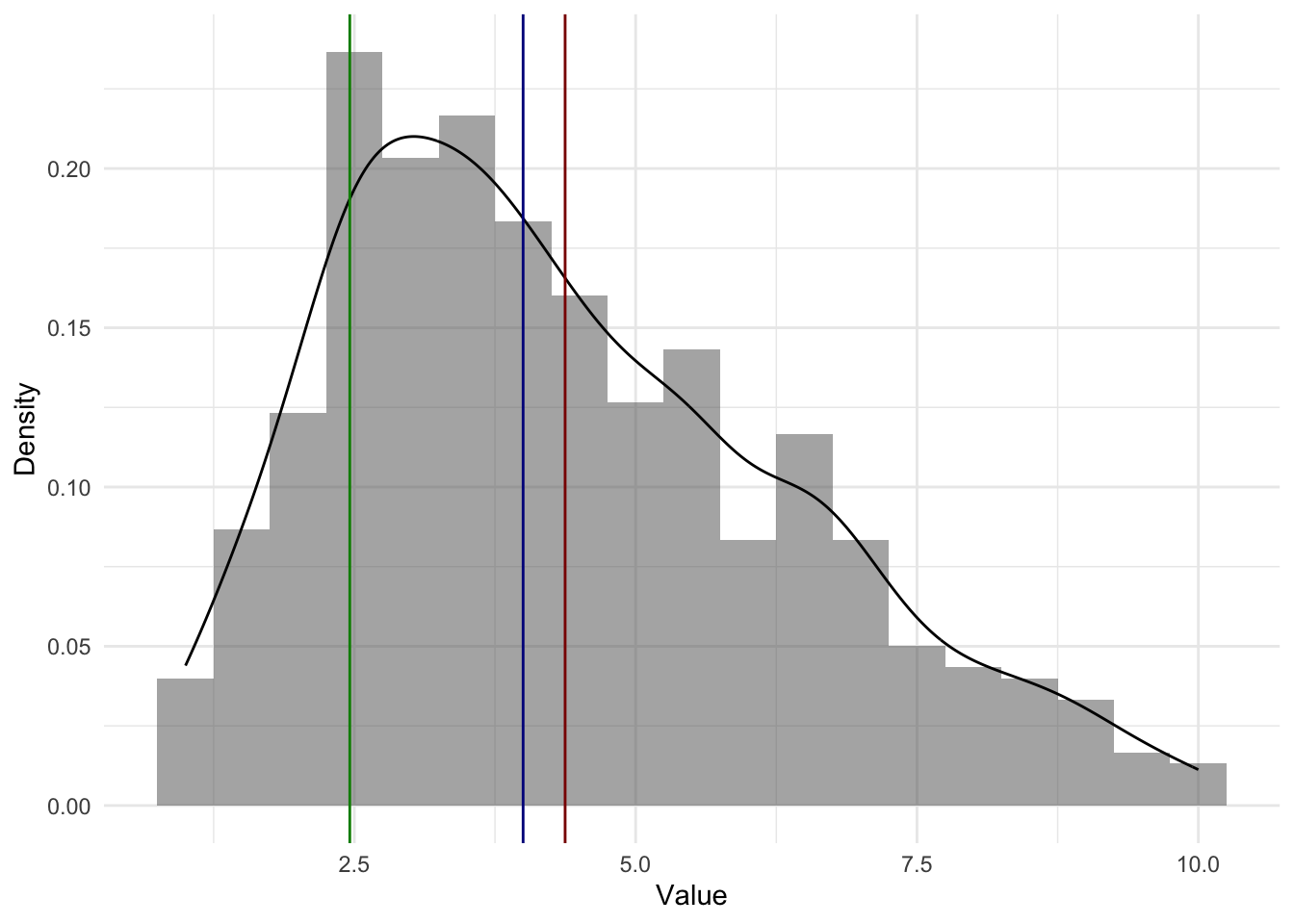
Мы подошли вплотную к понятиям, которые можно (и мы будем) непосредственно применять на даннных. Чтобы сделать эти понятия близкими к реальности, возьмем реальный датасет (собранные данные), на котором будем дальше работать. В качестве примера возьмем датасет с kaggle https://www.kaggle.com/datasets/uciml/student-alcohol-consumption. Это – данные из двух португальских школ (скорее колледжей) с подробной социо-демографической информации о студентах, включая ту, как они учатся по математике и португальскому языку и как часто пьют алкоголь. Этот датасет я взяла, так как он содержит переменные разного типа данных в разных шкалах (и шкала отношений, например, возраст, и порядковая шкала, например, рейтинггования образования мамы или папы или поддержка в семье).

kable(students[1:10,]) %>% scroll_box(width = "100%")
student school sex age address famsize Pstatus Medu Fedu Mjob Fjob reason guardian traveltime studytime failures schoolsup famsup paid_mat activities nursery higher internet romantic famrel freetime goout Dalc Walc health absences_mat G1_mat G2_mat G3_mat paid_por absences_por G1_por G2_por G3_por G_mat G_por ansences_mat_groups ansences_por_groups
id1 GP F 18 U GT3 A 4 4 at_home teacher course mother 2 2 0 yes no no no yes yes no no 4 3 4 1 1 3 6 5 6 6 no 4 0 11 11 5.666667 7.333333 middle less
id2 GP F 17 U GT3 T 1 1 at_home other course father 1 2 0 no yes no no no yes yes no 5 3 3 1 1 3 4 5 5 6 no 2 9 11 11 5.333333 10.333333 less less
id4 GP F 15 U GT3 T 4 2 health services home mother 1 3 0 no yes yes yes yes yes yes yes 3 2 2 1 1 5 2 15 14 15 no 0 14 14 14 14.666667 14.000000 less less
id5 GP F 16 U GT3 T 3 3 other other home father 1 2 0 no yes yes no yes yes no no 4 3 2 1 2 5 4 6 10 10 no 0 11 13 13 8.666667 12.333333 less less
id6 GP M 16 U LE3 T 4 3 services other reputation mother 1 2 0 no yes yes yes yes yes yes no 5 4 2 1 2 5 10 15 15 15 no 6 12 12 13 15.000000 12.333333 middle middle
id7 GP M 16 U LE3 T 2 2 other other home mother 1 2 0 no no no no yes yes yes no 4 4 4 1 1 3 0 12 12 11 no 0 13 12 13 11.666667 12.666667 less less
id8 GP F 17 U GT3 A 4 4 other teacher home mother 2 2 0 yes yes no no yes yes no no 4 1 4 1 1 1 6 6 5 6 no 2 10 13 13 5.666667 12.000000 middle less
id9 GP M 15 U LE3 A 3 2 services other home mother 1 2 0 no yes yes no yes yes yes no 4 2 2 1 1 1 0 16 18 19 no 0 15 16 17 17.666667 16.000000 less less
id10 GP M 15 U GT3 T 3 4 other other home mother 1 2 0 no yes yes yes yes yes yes no 5 5 1 1 1 5 0 14 15 15 no 0 12 12 13 14.666667 12.333333 less less
id11 GP F 15 U GT3 T 4 4 teacher health reputation mother 1 2 0 no yes yes no yes yes yes no 3 3 3 1 2 2 0 10 8 9 no 2 14 14 14 9.000000 14.000000 less less 
students %>% 
  ggplot(aes(x=age)) +
  geom_histogram(binwidth = 1) +
  geom_density(aes(x = age)) +
  theme_minimal()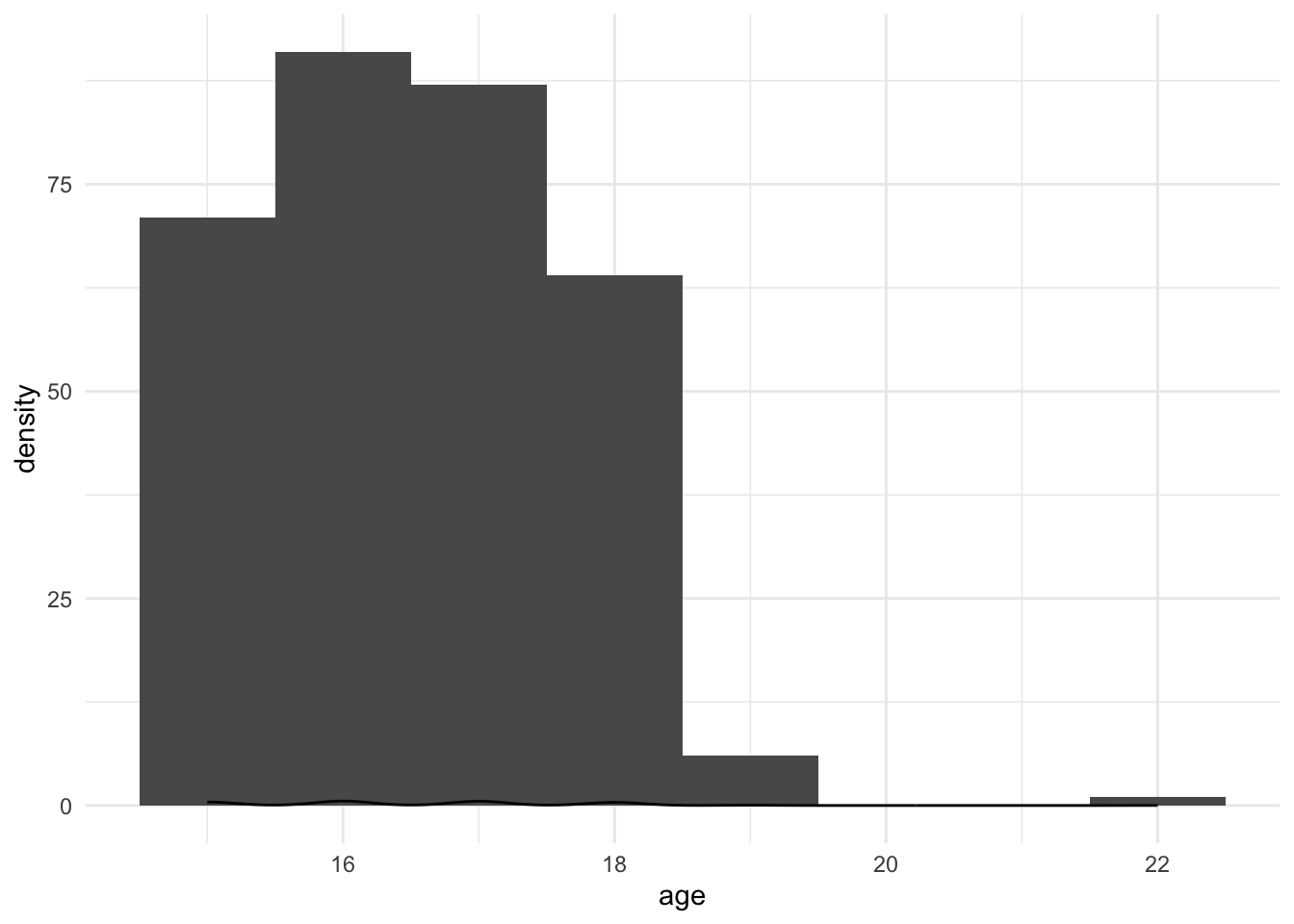

table(students$age)
## 
## 15 16 17 18 19 22 
## 71 91 87 64  6  1
prop.table(table(students$age))
## 
##       15       16       17       18       19       22 
## 0.221875 0.284375 0.271875 0.200000 0.018750 0.003125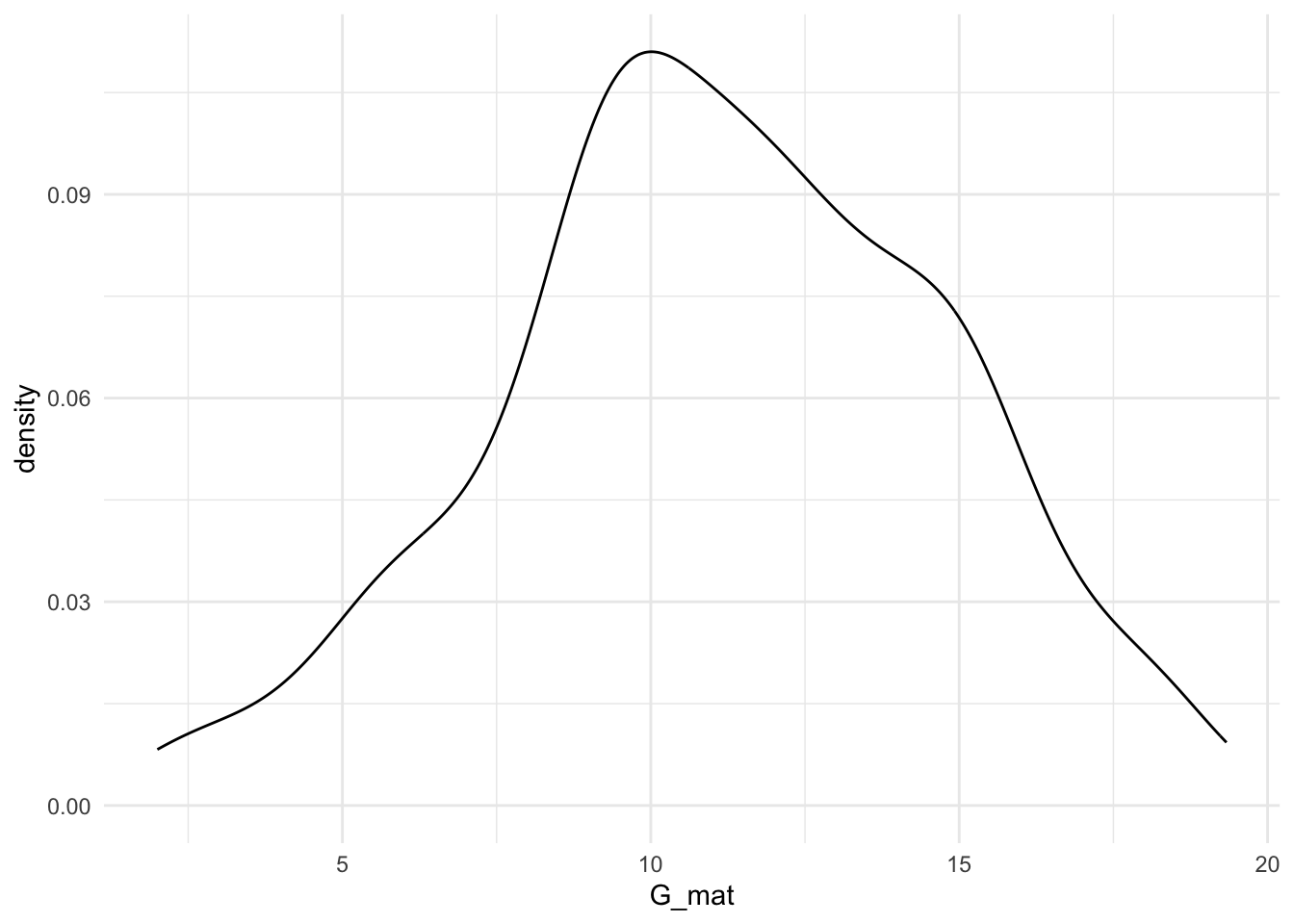
# round(prop.table(table(students$age, students$Walc), 1), 2)
mean(students$age)
## [1] 16.525
median(students$age)
## [1] 16
mode(students$age)
## [1] 16
students %>% 
  ggplot(aes(x=G_mat)) +
  geom_density() +
  theme_minimal()

mean(students$G_mat)
## [1] 11.16979
median(students$G_mat)
## [1] 11
table(students$Mjob)
## 
##  at_home   health    other services  teacher 
##       44       30      116       75       55
prop.table(table(students$Mjob))
## 
##  at_home   health    other services  teacher 
## 0.137500 0.093750 0.362500 0.234375 0.171875
mode(students$Mjob)
## [1] "other"

6.2 Квантили, квартили и перцентили

Мы выяснили, что медиана делит распределение пополам. Это удобно. Например, чтобы оценить, ниже / выше какого значения находится первая или вторая половина данных.

Такие вопросы возникают достаточно часто, и не только про половину данных, а про определенные кусочки данных. Квантили – общее обозначение для точек, которые делят распределение на равные по объему данных кусочки – например, на кусочки по десять процентов.

Децили – частные случаи квантилей, 9 точек, которые делят все распределение на 10 равных частей. Таким образом, в каждой части оказывается 10% данных.

Перцентили – частные случаи квантилей, 99 точек, которые делят все распределение на 100 равных частей. Таким образом, в каждой части оказывается 1% данных.

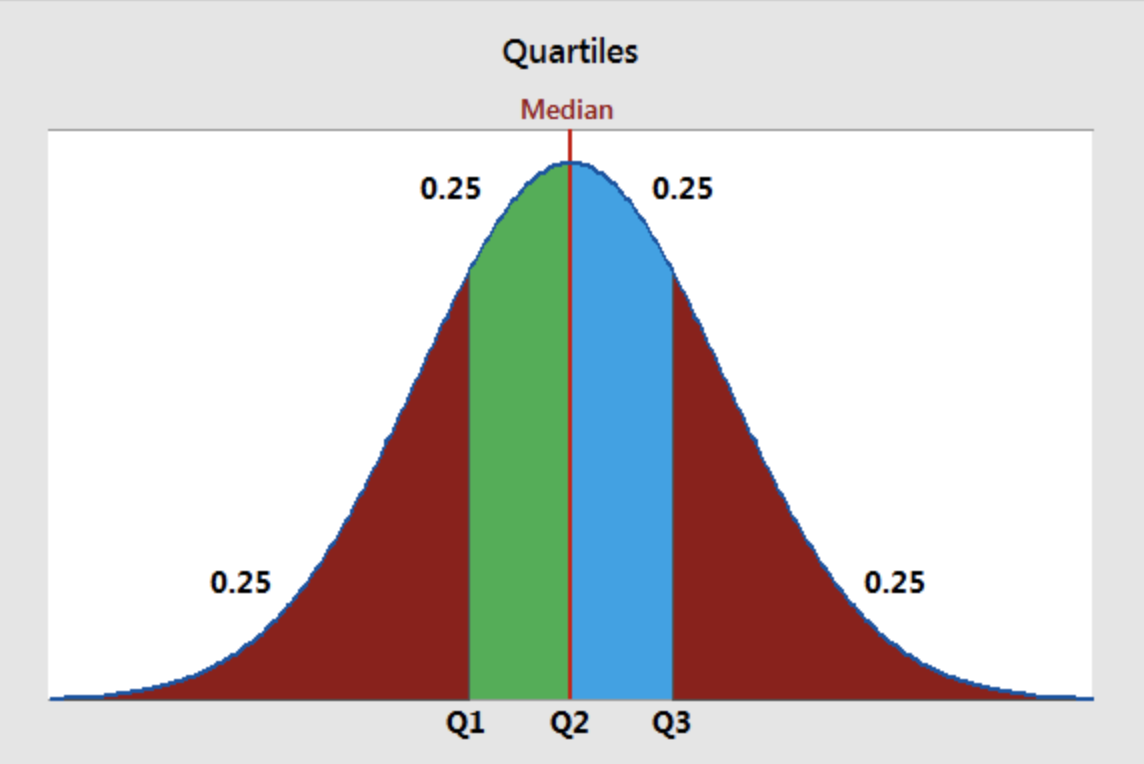
Квартили – частные случаи квантилей, делят все распределение на четыре части, по 25% данных. То есть, всего квартителей 4, и они обозначаются буквой Q: Q1, Q2, Q3, Q4.

Получается, что:

  • слева от первого (нижнего) квартиля \(Q_1\) лежит 25% наблюдений
  • слева от второго (среднего) квартиля (медианы) \(Q_2\) лежит 50% наблюдений
  • слева от третьего (верхнего) квартиля \(Q_3\) лежит 75% наблюдений

knitr::include_graphics("docs/images/quartiles-2.png")

6.3 Меры вариативности (изменчивости)

Помимо мер центральной тенденции – меры вариативности, они же меры изменчивости или разброса. Вариативность – изменчивость значений, как сильно разнятся данные от наблюдения к наблюдению в рамках выборки.

Допустим, вы рбнаружили, что ваш показатель эритроцитов в крови равен 3,8 * 10 при норме 4*10. Насколько сильное это отклонение?

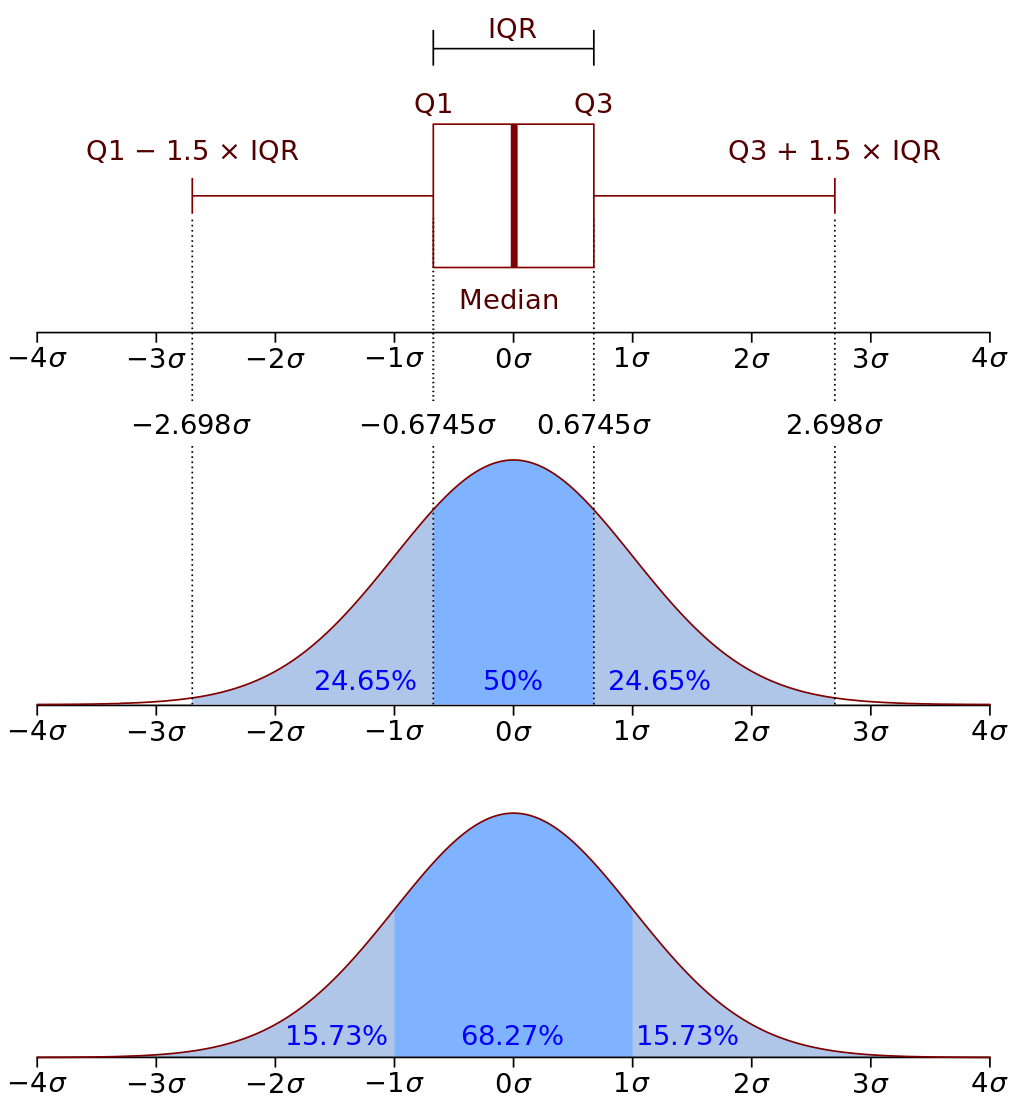
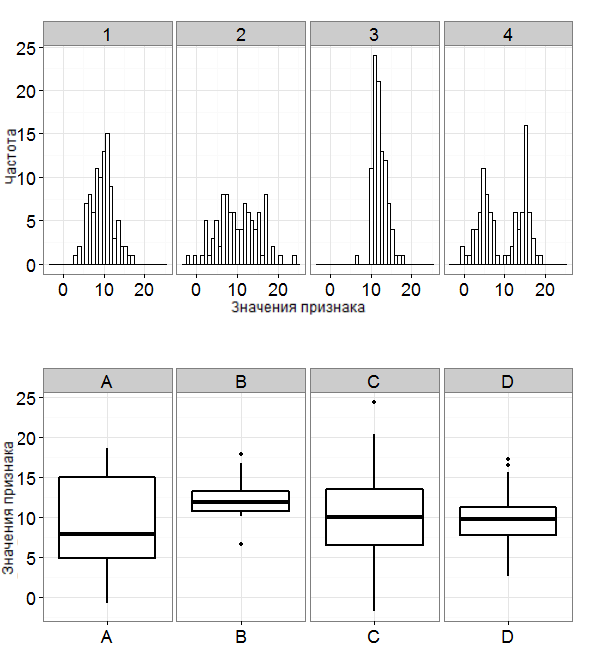
Зачем они нужны? Разве недостаточно только мер центральной тенденции для описания распределения? Нет, недостаточно. В то время как меры ЦТ показывают, куда тяготяют наши данные, где их “центр масс”, то есть каким одним числом можно охарактеризовать наши данные в общем – меры изменчивость показывают, а насколько большой разброс в наших данных, насколько каждое из наших наблюдений лежит близко к среднему?

Меры центральной тенденции могут совпадать, хотя меры изменчивость значительно отличаться, например

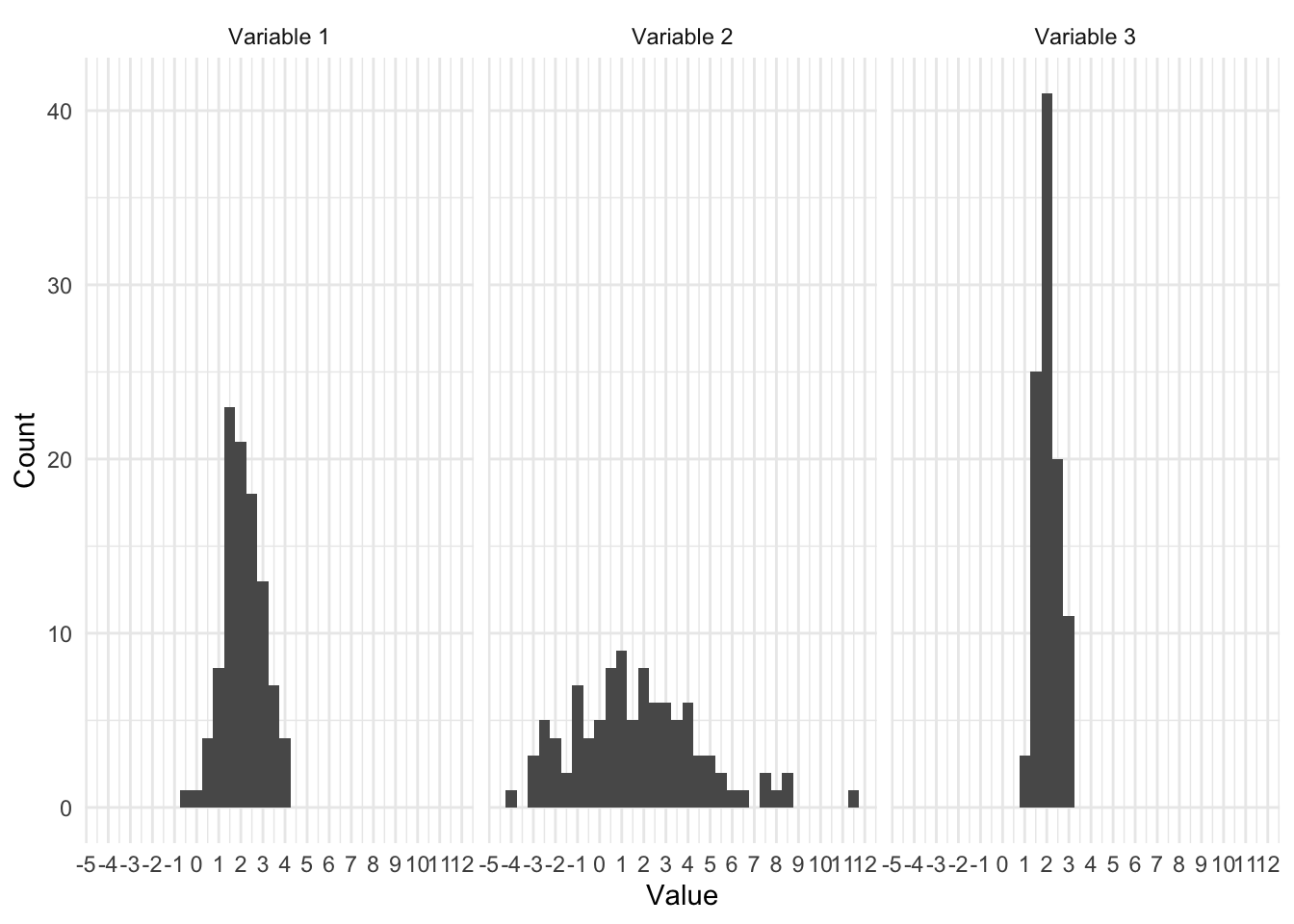
Изображения из учебника Антона Ангельгардта

Эти распределения очень разные, но все-таки они вместе если посмотреть на их средние – они будут одинаковыми

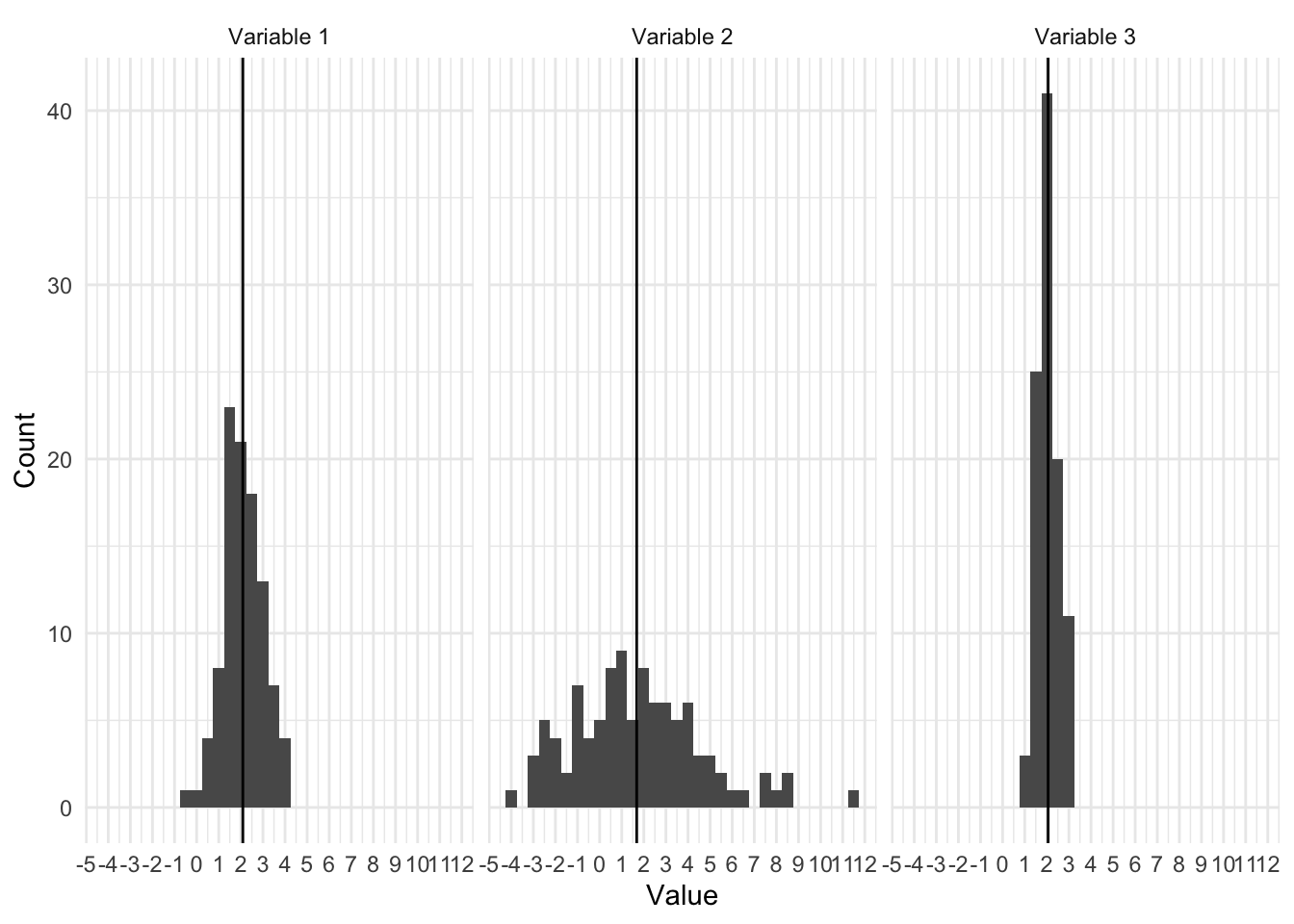
6.3.1 Размах, стандартное отклонение и дисперсия

Размах (range) – разница между максимальным и минимальным значением в выборке, \(x_{max}-x_{min}\)

sample_data1
##  [1] 49 37  1 25 10 36 18 24  7 45 47
range(sample_data1)
## [1]  1 49

Здесь показаны минимальное и максимальные значения, чтобы посчитать размах, нужно из максимальнго вычесть минимальное. И как можно понять, размах очень чувствителен к выбросам – если добавить значение “3000” к этой выборке, размах изменится кардинально.

Мы уже слышали о стандартном отклонении (как минимум, оно фигурирует в формуле нормального распределения). Теперь познакомимся с ним ближе и попробуем его вывести.

Так как если мы будем считать отклонение каждого наблюдения от среднего и попытаемся их усреднить, то получим ноль – значит, нам нужен другой подход к оценке отклонения. Если мы хотим избавиться от проблемы получения нуля, то у нас есть обычно два варианта: взять значения по модулю или возвести их в квадрат. Для получения оценки отклонения воспользовались вторым вариантом и ввели еще одну важную меру вариативности для – дисперсию.

Дисперсия (variance) – мера вариативности, которая являются квадрату стандартного отклонения и считается по формуле \(D = \dfrac{\sum_{i=1}^{n}(x_i - \bar x)^2}{n}\)

Чем больше ваиативность в данных, тем больше (пропорционально квадрату отклонений) дисперсия.

Важный момент – это формула дисперсии для генеральной совокупности. Для выборочной дисперсии количество степеней свободы умньшается на единицу, поэтому формула примет такой вид \(D = \dfrac{\sum_{i=1}^{n}(x_i - \bar x)^2}{n-1}\)

Стандартное отклонение, оно же среднеквадратичное отклонение (standard deviation) – это среднее отклонение наблюдений от их среднего означения. Оно рассчитывается как квадратный корень из дисперсии: \(sd = \sqrt{\dfrac{\sum_{i=1}^{n}(x_i - \bar x)^2}{n-1}}\)

Свойства дисперсии и стандартного отклонения

Так же, как и для среднего, для дисперсии / стандартного отклонения есть важные свойства

  1. Если к каждому значению выборки прибавить (или вычесть) одно и то же число (константу) \(c\), то дисперсия и стандартное отлокнение не изменятся: \(D_(x_i+c) = D\), \(sd_(x_i+c) = sd\)

  2. Если каждое значение выборки умножить (или разделить) одно и то же число \(c\), то дисперсия увеличится (уменьшится) в \(c^2\) раз \(D_(x_i \times c) = D \times c^2\), а реднее увеличится (или уменьшится) в \(c\) раз: \(sd_(x_i \times c) = sd \times c\)

  3. Если значения двух выборок не отличаются друг от друга, то у них равная дисперсия и стандартное отклонение

На примере с данными студентов:

range(students$age)
## [1] 15 22
range(students$G_mat)
## [1]  2.00000 19.33333
range(students$Walc)
## [1] 1 5
range(students$Mjob)
## [1] "at_home" "teacher"
sd(students$age)
## [1] 1.141687
sd(students$G_mat)
## [1] 3.559905
sd(students$Walc)
## [1] 1.264167

Межквартильный размах

6.4 Боксплот и вайолинплот

knitr::include_graphics("docs/images/Boxplot_vs_PDF.png")

knitr::include_graphics("docs/images/boxplots_hist.png")

library(viridis)
## Loading required package: viridisLite
students %>% 
  ggplot(aes(x=ansences_mat_groups, y = G_mat)) +
  geom_violin(aes(fill = ansences_mat_groups)) +
  geom_boxplot(aes(fill = ansences_mat_groups), width=.1) +
  scale_fill_viridis(discrete=TRUE) +
  theme_minimal()