8 Интвервальные оценки среднего

До этого мы пыталась оценить генеральную совокупность, подставив вместо неизвестных значений среднего и стандартного отклонения генеральной совокупности – выборочные. Это точечные оценки.

	Генеральная совокупность	Выборка
Среднее (математическое ожидание)	\(\mu\)	M, \(\overline X\)
Стандартное отклонение	\(\sigma\)	s, sd

Однако, это не единственный способ узнать что-то о генеральной совокупности. Вместо того, чтобы оценить точно, мы можем использовать еще и интервалы – то есть сказать, что среднее генеральной совокупности с заданной вероятностью лежит в таком-то интервале. Это – интервальный подход к оценке генеральной совокупности, и он будет нам сильно полезен, когда мы перейдем к статистике вывода.

8.1 Центральная предельная теорема

Центральная предельная теорема – важное понятие в статистике, применимое к исследованиям в социальных науках. Мы уже выучили, что переменные, с которыми мы работаем – это случайные величины [#random-variable]. Именно этот факт позволяет нам вычислять могие параметры по тем формулам, которые мы используем: если бы мы работали не с случайными величинами, у нас была бы совсем другая статистика (кажется, куда более сложная)!

В общем виде, ее можно сформулировать так:

Значения признака, являющегося случайной величиной (чье значение нельзя предсказать точно) и подтверженного влиянию сразу нескольких независимых факторов, распределены нормально.

Именно поэтому для многих признаков, с которыми мы работаем (рост, вес, ответы на опросник и тд) мы ожидаем именно нормального распределения.

Из нее есть важное следствие: > Если мы будем извлекать много выборок из генеральной совокупности (проводить много одинаковых исследований), то выборочные средние этих выборок будут распределены нормально

Например, мы изучаем выгорание среди преподавателей, но вместо одного исследования провели сто, и в каждом исследовании посчитали выборочное среднее. Такое распредление и называется распределением выборочных средних, и оно будет распределено нормально. Причем чем больше выборок мы будем извлекать – тем более будет стемиться к нормальному это распределение, и тем ближе к среднему генеральной совокупности будет ближе среднее распределения выборочных средних (да, тут очень много слов “средние” и “распределения”, но постарайтесь не запутаться).

mean(means_from_samples)

## [1] 100.024

sd(means_from_samples)

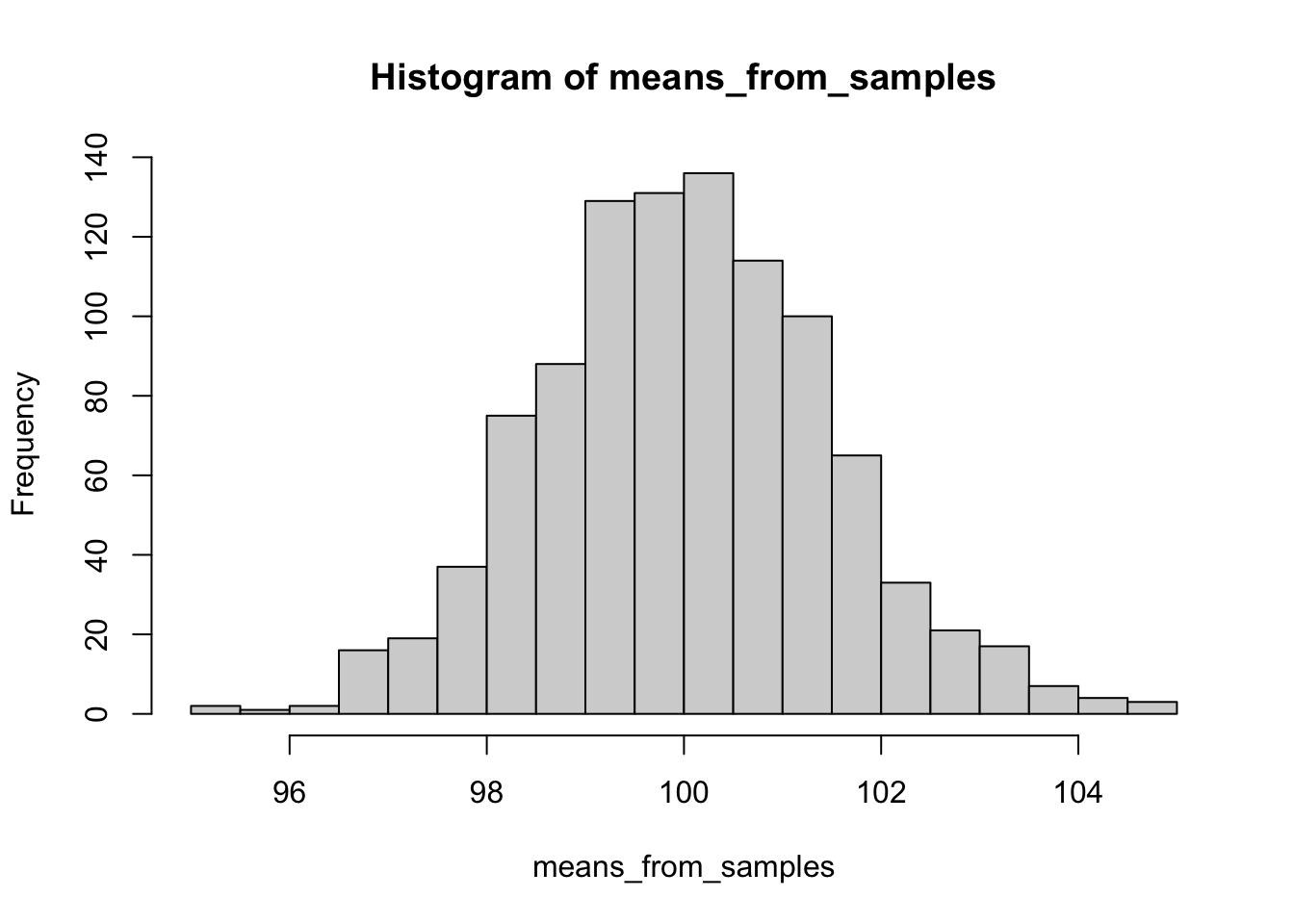
## [1] 1.485935

Визуализацию принципов работы этого важного следствия ЦПТ можно посмотреть здесь https://gallery.shinyapps.io/CLT_mean/. Меняя число извлеченных из ГС выборок можно посмотреть, как выборочные распределения становятся ближе к нормальному распредедению, а их среднее – к среднему генеральной совокупности. Эта визуализация наглядно показывает, как количество наблюдений в выборке и количество извлекаемых выборок влияет на оценку среднего ГС. Допустим распределение данных в ГС выглядит так

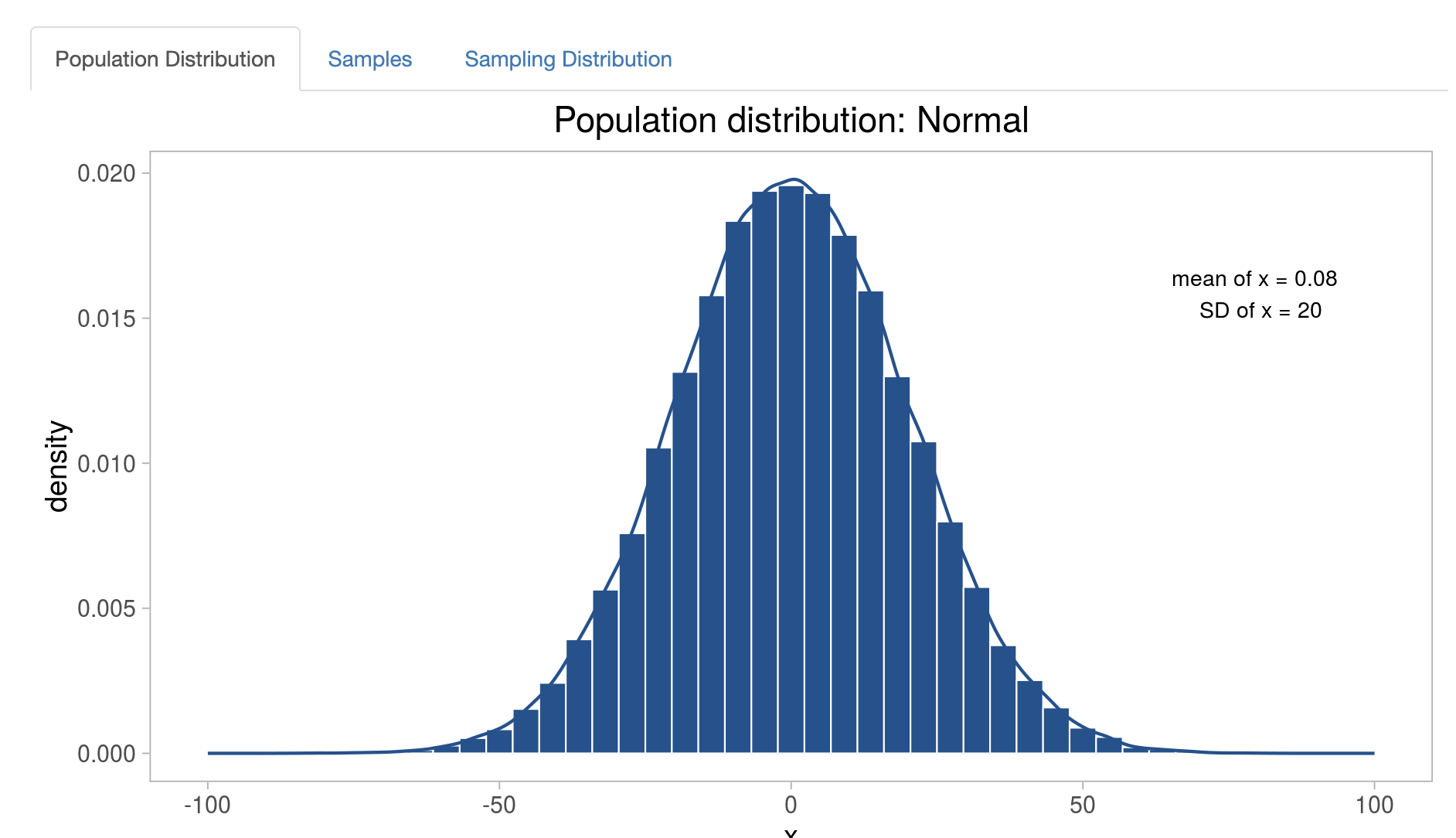
Если мы будем извлекать из него 10 выборок по 30 наблюдений, то они будут выглядеть так

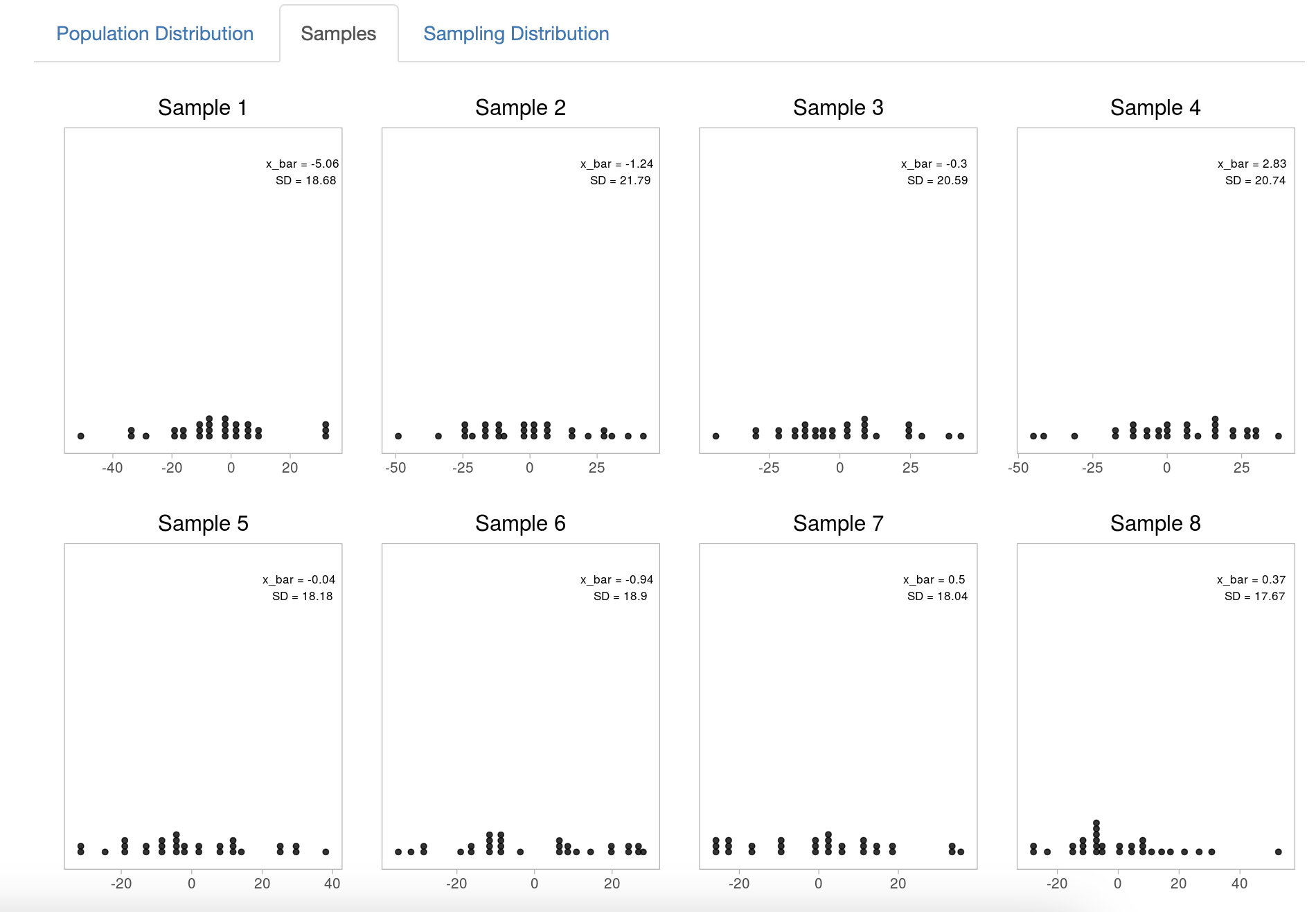
А распределение этих 10 выборочных средних – так

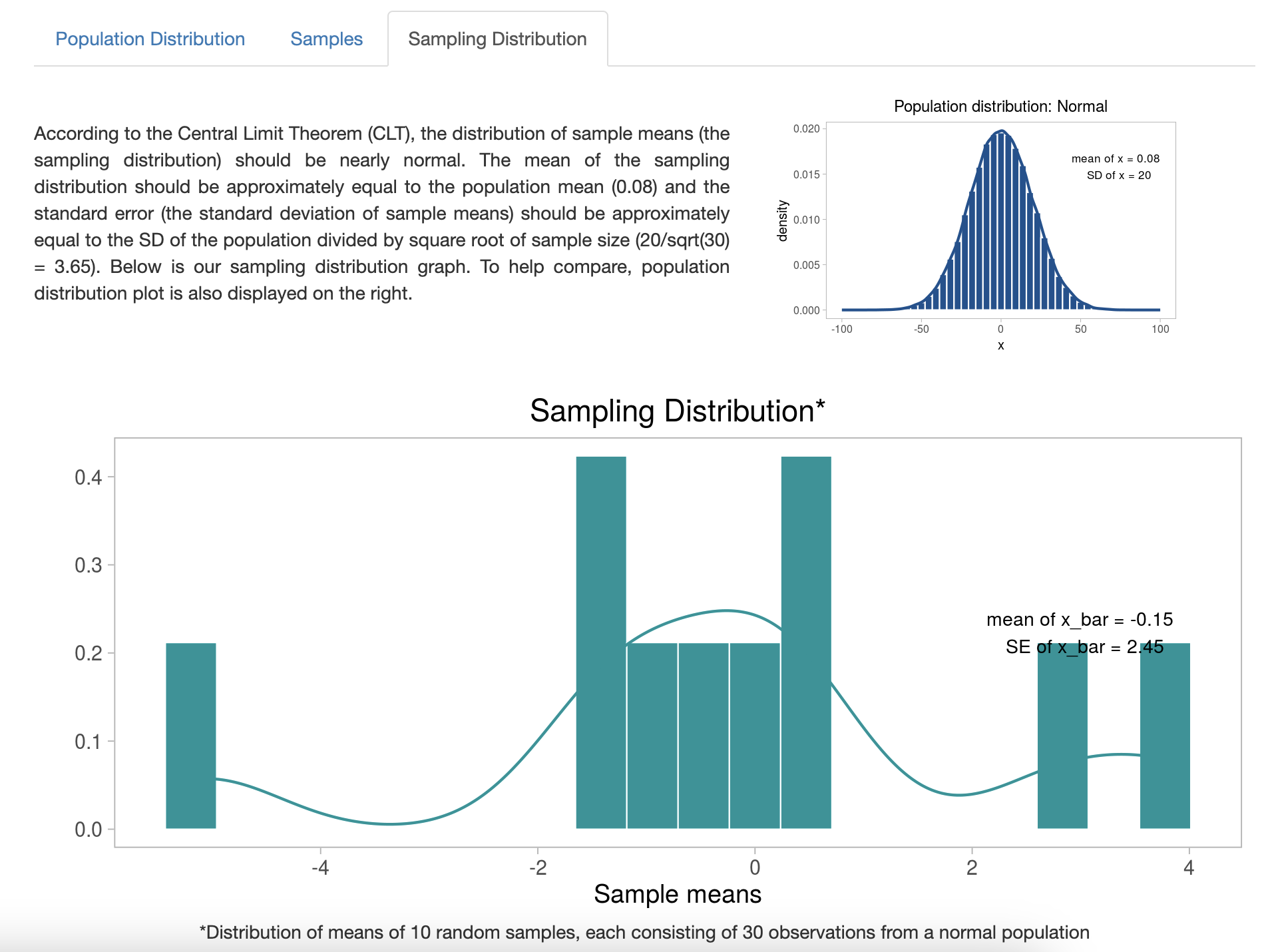
При этом, увеличивая размер выборок с 30 в 3 раза, наши выборки будут больше походить на распределние ГС

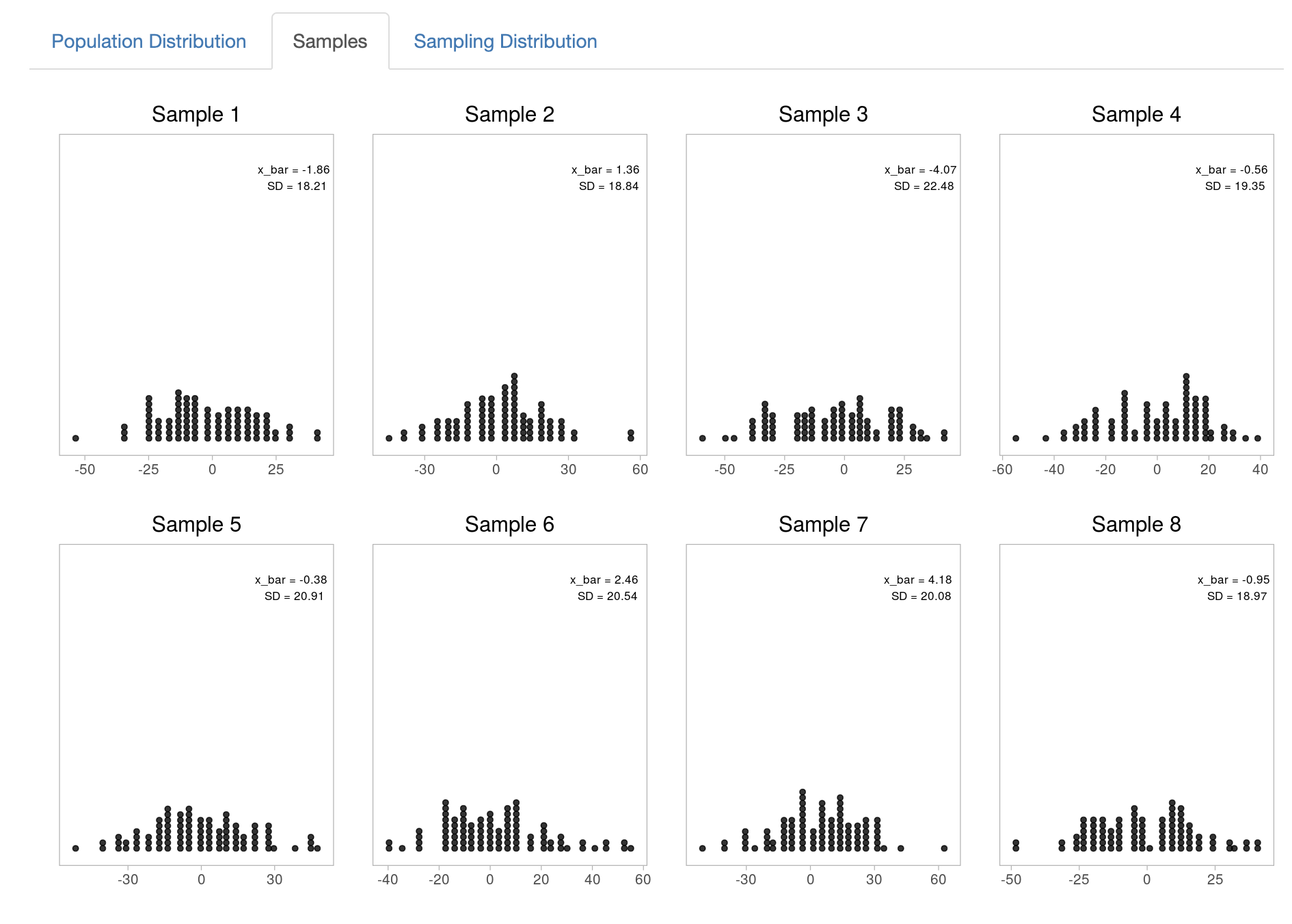
А увеличив само число выборок до 87 – распределение выборочных средних будет уже более похоже на нормальное

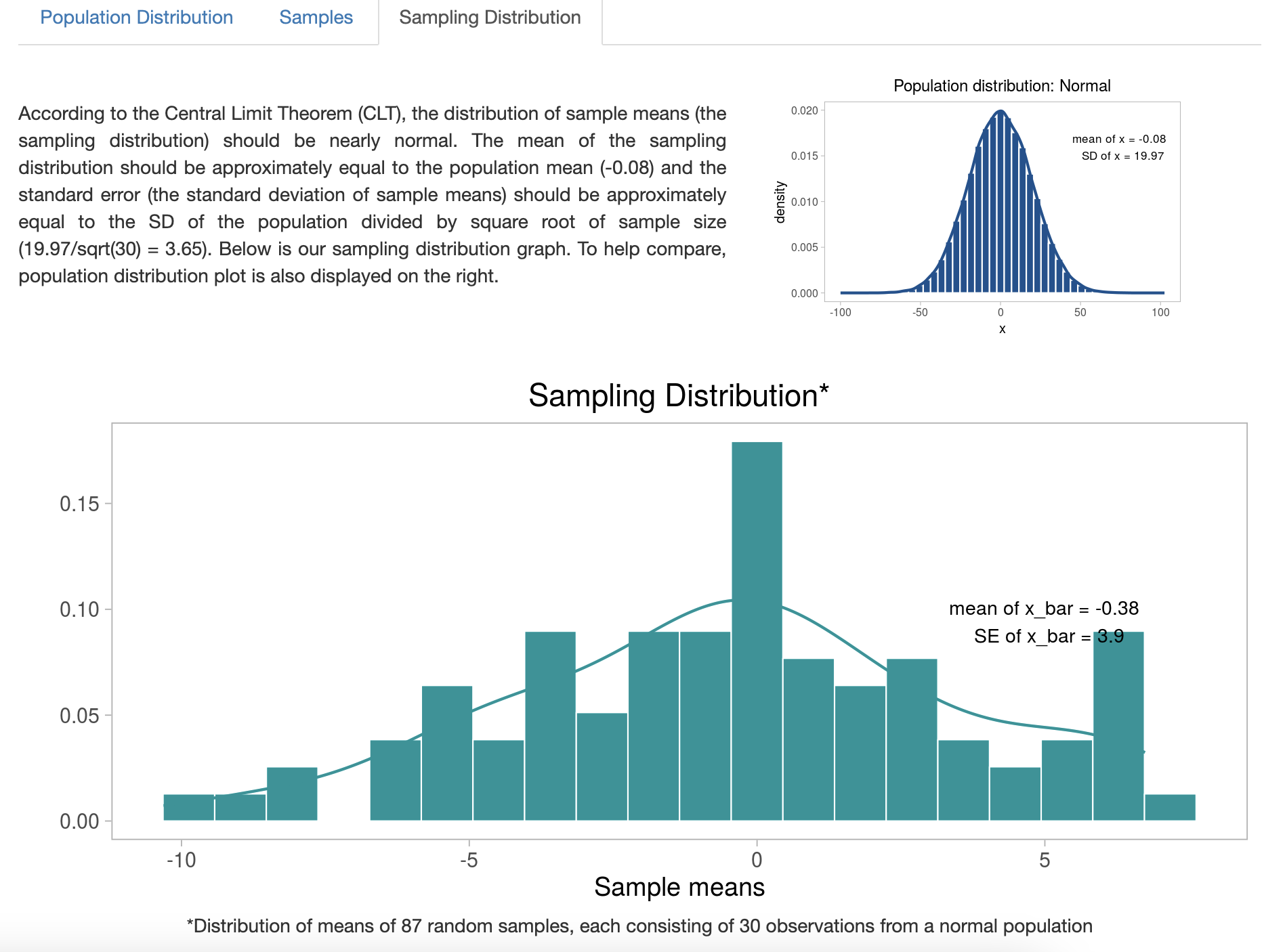
Центральная предельная теорема имеет очень полезный смысл для научных исследований: гораздо большее доверие вызывают исследования, проведенные несколько раз при одних и тех же или похожих условиях, так как в этом случае можно провести мета-анализ и рассчитать средние параметы этих исследований – они будут гораздо сильнее отражать ГС, чем каждое отдельно взятое исследоваание.

Если про cтандартное отклонение такого распределение выборочных средних мы можем сказать, что оно приближается к среднему ГС с увеличением числа выборок, то стандартное отклонение этого распределение называется стандартной ошибкой среднего (standard error of the mean (s.e.m. или se) и показывает, наасколько наши выборки отклонились от ГС. Стандартная ошибка среднего часто обозначается как se и вычисляется по формуле \(\sigma_{\overline{x}}=se= \frac{\sigma} {\sqrt{n}}\) или, используя выборочное стандартное отклонение по одной выборке \(se= \frac{sd} {\sqrt{n}}\)

Стандартную ошибку среднего можно рассматривать как ошибку репрезентативности: насколько сильно выборочные параметы нашей выборки (среднее и стандартное отклонение) могут отличаться от ГС. Чем меньше se, тем ближе наша выборка к генеральной совокупности.

\(se = \frac{\sigma}{\sqrt{n}} ≈ \frac{sd}{\sqrt{n}}\)

Стандартная ошибка среднего – необходима для того, чтобы сделать интервльную оценку среднего ГС и рассчитать доверительный интервал для среднего ГС.

8.2 Доверительный интервал

Мы рассмотрели описательные статистики: меры центральной тенденции и меры вариативности переменной. Это были точечные оценки: мы используем эти величины, чтобы описать наши данные, перейти от таблички к одному или нескольким числам. Помимо точечных оценок используются также интервальные – если мы хотим получить не конкретное число, а интервал, в котором будет содержаться интересующий нас параметр (например, среднее ГС).

Доверительный интервал показывает, в каких границах от выборочного среднего находится среднее генеральной совокупности. Например, если на моей выборке я получила среднее значение выгорания равное 13.5 (что бы это ни значило), то я, используя эти выборочные данные, могу указать границы, которые будут содержать среднее уже генеральной совокупности: mean ± интервальная оценка, например \(13.5 ± 2.4 = [13.5 - 2.4, 13.5 + 2.4]\). В этом суть интервальных оценок ГС.

Доверительный интервал может обозначаться как CI (confidence interval)

Доверительному интервалу соответствует определенный процент – как правило, ровно те проценты, которые мы уже выучили – сколько данных лежат в ± 1 стандартном отклонении от среднего (68%), ± 2 sd (95%) и ± ± 3 sd (99,7%) . Это – процент выборок из генеральной совокупности, доверительные интервалы которых будут содержать среднее генеральной совкупности. Здесь тоже на помощь приходит красивая визуализация https://rpsychologist.com/d3/ci/. Меняя доверительный интервал (например, с 95% на 68%), можем заметить, что наши выборки (горизонтальные линии) стали реже ловить среднее генеральной совокупности (вертикальная пунктирная линяя), а средние этих выборок (синие точки) откланяются от среднего ГС дальше и чаще

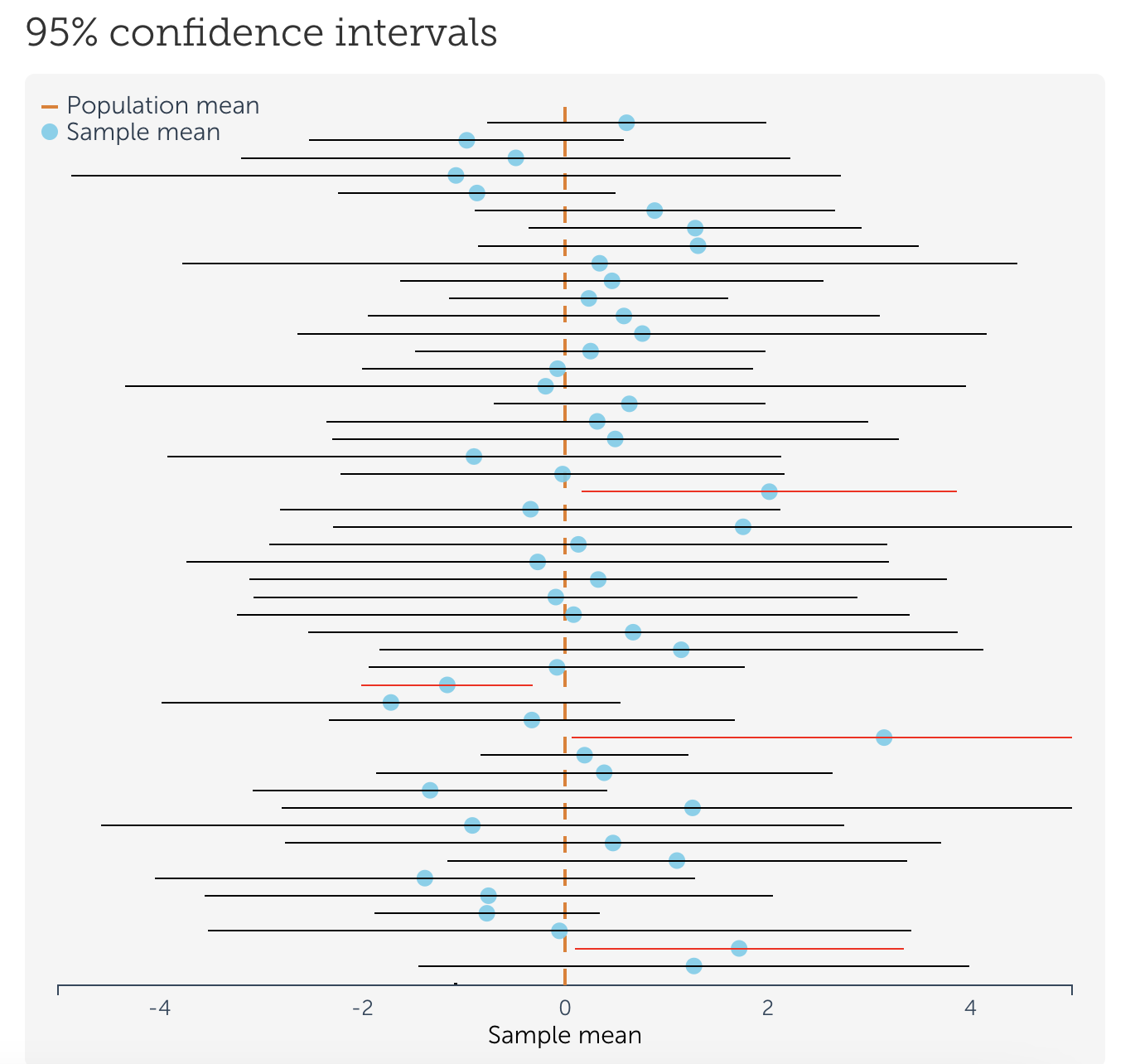
Доверительный интервал пригодится нам и далее в статистике вывода, так как вообще-то уже позволяет оценить правомерность того или иного статистического высказывания относительно выборочного среднего. Он считается с помощью Z-оценки и стандартной ошибки среднего, только здесь мы делаем как бы обратную стандартизацию – до этого мы вычисляли Z-оценку для заданного числа из выборки и смотрели, какой процент данных соответствует этой оценке, а теперь мы смотрим на процнт и находим для него Z-оценку.

\(CI_\%: \bar X \pm Z_\% \times \mathrm{se} \\\), где \(\bar X\) – выборочное среднее, $Z_% $ – Z-оценка для заданного процента данных, \(se\) – стандартная ошибка среднего.

Важно помнить ключевые значения:

• \(Z_{95\%} = 1.96 ≈ 2\), значит \(CI_{95\%} = \pm 1.96 \times \mathrm{se} ≈ \pm 2 \times \mathrm{se}\)

• \(Z_{99\%} = 2.576\), значит \(CI_{99\%} = \pm 2.576 \times \mathrm{se}\)

Если исходить из целых значений Z-оценки, можно встретить еще такие доверительные интервалы:

• \(Z_{68\%} = 1\), значит \(CI_{68\%} = \pm 1 \times \mathrm{se}\)

• \(Z_{99.7\%} = 3\), значит \(CI_{99.7\%} = \pm 3 \times \mathrm{se}\)

Чаще всего на практике используется 95%-доверительный интервал, и в следующем блоке про статистический вывод мы поймем, почему.

Задача на доверительный интервал:

Исследование семейных пар в России (объем выборки составил 100 семейных пар), в которых есть дети подросткового возраста, показало, что те пары, где отец и мать работают полный рабочий день, они проводят со своими детьми в среднем 15 часов свободного времени в неделю. Согласно данным проведенного исследования, стандартное отклонение оказалось равным 4,5 (ч). Можно ли на уровне доверия 0,99 утверждать, что в семьях, в которых работают и отец, и мать, в среднем в течение недели родители проводят с детьми подросткового возраста больше 14 часов?

Решение (попробуйте сначала решить сами!)

1. Сначала определеяем, о чем нас спрашивают в этой задаче: нам нужно посотроить доверительный интервал для выборочного среднего = 15 и сравнить его с числом 14: находится оно левее этого интервала, и тогда можно сказать, что родители проводят с детьми в среднем больше 14 часов, или 14 входит в этот интервал, и тогда это утверждение будет неверно

2. Вычисляем доверительный интервал CI (confidence interval): равен \(Z_{99\%} \times se\): Z-значение, при котором охватывается 99% даннных, равно 2.576. \(se = \frac{\sigma}{\sqrt{n}} = \frac{sd}{\sqrt{n}} = \frac{4.5}{\sqrt{100}} = 0.45\) Доверительный интервал равен \(Z_{99\%} \times se = 2.576 \times 0.45 ≈ 1.13\):

3. Таким образом, можем записать доверительный интервал: \(CI_{99\%} = \bar X \pm Z_\% \times \mathrm{se} = [15-1.13; 15+1.13] = [13.87;16.13]\). Сравним его с числом 14: видим, что 14 входит в этот интервал, то есть, утверждение, что родители проводят с детьми в среднем больше 14 часов на уровне доверия 0.99 – неверно.